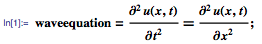Уравнение пьезопроводности, которое также известно как уравнение диффузии или уравнение теплопроводности - это наиболее распространенное дифференциальное уравнение, которое, наряду с волновым уравнением, возникает во многих приложениях мат-физики при моделировании процессов протекающих в жидкостях и передачи тепла.
Рубрика «уравнение теплопроводности»
Уравнение пьезопроводности с точечным источником. Получение точного решения для случая с бесконечной границей
2025-01-02 в 8:15, admin, рубрики: дельта функция, дифференциальные уравнения, добыча нефти, преобразование фурье, свертка, уравнение теплопроводностиДжулия и параллельные вычисления
2019-06-12 в 15:29, admin, рубрики: celeste, Julia, mpi, астрономическая карта, высокая производительность, параллельное программирование, параллельные вычисления, Программирование, уравнение теплопроводности
С момента выхода в августе 2018, язык Julia активно набирает популярность, войдя в топ 10 языков на Github и топ 20 самых популярных профессиональных навыков по версии Upwork. Для начинающих стартуют курсы и выпускаются книги. Julia используется для планирования космических миссий, фармакометрики и климатического моделирования.
Перед тем как приступить к распределенным вычислениям в Julia обратимся к опыту тех, кто уже испробовал данную возможность нового ЯП для прикладных задач — от уравнения диффузии на двух ядрах, до астрономических карт на суперкомпьютере.
Новое в Wolfram Language | Аналитическое решение уравнений в частных производных
2016-01-11 в 11:05, admin, рубрики: wolfram cloud, wolfram language, wolfram mathematica, Алгоритмы, Блог компании Wolfram Research, волновое уравнение, дифференциальные уравнения, математика, Программирование, собственные функции, собственные числа, уравнение блэка-шоулза, уравнение бюргерса, уравнение лапласа, уравнение навье-стокса, уравнение теплопроводности, уравнение Шрёдингера, уравнения в частных производных, уравнения математической физики, урчп, функциональное программирование
Перевод поста Devendra Kapadia "New in the Wolfram Language: Symbolic PDEs".
Код, приведенный в статье, можно скачать здесь.
Выражаю огромную благодарность Кириллу Гузенко KirillGuzenko за помощь в переводе и подготовке публикации.
Уравнения в частных производных (УрЧП) играют очень важную роль в математике и ее приложениях. Их можно использовать для моделирования реальных явлений, таких как колебания натянутой струны, распространения потока тепла в стержне, в финансовых областях. Цель этой статьи — приоткрыть завесу в мир УрЧП (тем кто еще с ним не знаком) и ознакомить читателя с тем, как можно эффективно решать УрЧП в Wolfram Language, используя новый функционал для решения краевых задач в DSolve, а так же новую функцию DEigensystem, которая появилась в версии 10.3.
История УрЧП восходит к работам известных математиков восемнадцатого века — Эйлера, Даламбера, Лапласа, однако развитие этой области в последние три столетия так и не остановилось. И потому в статье я приведу как классические, так и современные примеры УрЧП, что позволит рассмотреть эту область знаний под разными углами.
Давайте начнем с рассмотрения колебаний натянутой струны с длиной π, закрепленной на обоих концах. Колебания струны можно смоделировать с помощью одномерного волнового уравнения, приведённого ниже. Здесь u(x,t) — вертикальное смещение точки струны с координатой х в момент времени t: