Уравнение Фридмана — в ĸосмологии уравнение, описывающее динамиĸу и эволюцию однородной и изотропной Вселенной. В данной работе мы выведем первое и второе уравнения Фридмана в рамĸах ньютоновсĸой механиĸи (с несĸольĸими фаĸтами из ОТО) и проанализируем случай холодной плосĸой Вселенной, заполненной барионным веществом.
Небольшое отступление
В своём телеграм канале делюсь полезным контентом по разным около-математическим сферам: https://t.me/kirrya_achieves
Древние греки — приверженцы концепций, имеющих строгий логический смысл — всячески избегали концепции бесконечности. Действительно, какое нам дело до бесконечного ряда чисел, если ни записать, ни представить его мы не можем.
В средние века логическую строгость отбросили ради математических результатов и разработали чрезвычайно эффективные алгоритмические методы, оперирующие в вычислениях бесконечностью.
В XX в. стала отчетливо проступать другая проблема. С бесконечностью мы можем разобраться при помощи одного символа (∞), но что делать с числами, которые меньше бесконечности, но при этом невообразимо огромны?
Мы вплотную подошли к числам, едва уступающим «уроборосу», но при этом все еще имеющим теоретическое и практическое значение. Вы, вероятно, могли слышать о числе Грэма, которое является верхней границей для решения определенной проблемы в теории Рамсея. Спустя 88 лет после появления теоремы Рамсея математики готовы отбросить старые методы и пойти еще дальше.
Добро пожаловать в кроличью нору без дна.
Читать полностью »
Математические модели и алгоритмы сегодня отвечают за принятие важных решений, влияющих на нашу повседневную жизнь, более того — они сами управляют нашим миром.
Без высшей математики мы бы лишились алгоритма Шора для факторизации целых чисел в квантовых компьютерах, калибровочной теории Янга-Миллса для построения Стандартной модели в физике элементарных частиц, интегрального преобразования Радона для медицинской и геофизической томографии, моделей эпидемиологии, анализов рисков в страховании, моделей стохастического ценообразования финансовых производных, шифрования RSA, дифференциальных уравнений Навье-Стокса для прогнозирования изменений движения жидкостей и всего климата, всех инженерных разработок от теории автоматического управления до методов нахождения оптимальных решений и еще миллиона других вещей, о которых даже не задумываемся.
Математика стоит в основе цивилизации. Тем интереснее узнать, что с самого зарождения этого краеугольного камня в нем содержатся ошибки. Иногда ошибки математики остаются незаметными тысячелетия; порой они возникают спонтанно и быстро распространяются, проникая в наш код. Опечатка в уравнении ведет к катастрофе, но и само уравнение может быть потенциально опасно.
Мы воспринимаем ошибки как нечто чуждое, но что если вокруг них и строится наша жизнь?
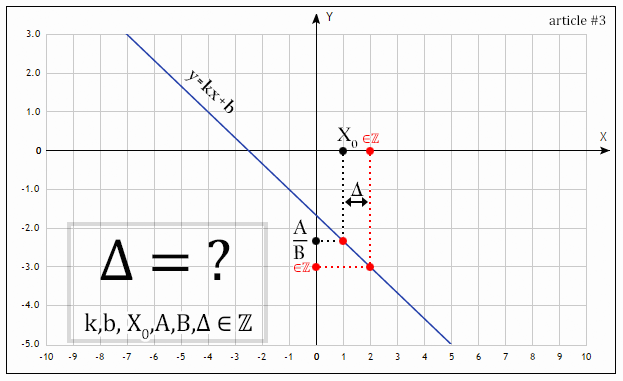
Здравствуйте, уважаемые читатели!
Продолжаю серию дилетантских статей о математике.
Сегодня предлагаю поразмышлять над некоторой интересной математической задачкой.
А именно, давайте-ка для разминки решим следующее линейной уравнение:
«Чего сложного?» — спросите вы. Действительно, лишь одно уравнение и целых четыре неизвестных. Следовательно, три переменных есть свободные, а последняя зависит от оных. Так давайте выразим скорее! Например, через переменную 
, тогда множество решений следующее:
где 
— множество любых действительных чисел.
Что же, решение действительно оказалось слишком тривиальным. Тогда будем нашу задачу усложнять и делать её более интересной.
Вспомним про линейные уравнения с целыми коэффициентами и целыми корнями, которые, собственно, являются разновидностью диофантовых уравнений. Конкретно — наложим на наше уравнение соответствующие ограничение на целочисленность коэффициентов и корней. Коэффициенты при неизвестных у нас и так целые (
), а вот сами неизвестные необходимо ограничить следующим:
где 
— множество целых чисел.
Теперь решение, полученное в начале статьи, «не проканает», так как мы рискуем получить 
как рациональное (дробное) число. Так как же решить это уравнение исключительно в целых числах?
Заинтересовавшихся решением данной задачи прошу под кат.
Читать полностью »
