Рубрика «цепи маркова»

В предыдущей статье про 2048 мы использовали цепи Маркова, чтобы выяснить, что в среднем для победы нужно не менее 938,8 ходов, а также исследовали с помощью комбинаторики и полного перебора количество возможных конфигураций поля игры.

В этом посте мы используем математический аппарат под названием «марковский процесс принятия решений» для нахождения доказуемо оптимальных стратегий игры 2048 для полей размером 2x2 и 3x3, а также на доске 4x4 вплоть до тайла 64. Например, вот оптимальный игрок в игру 2x2 до тайла 32:

GIF

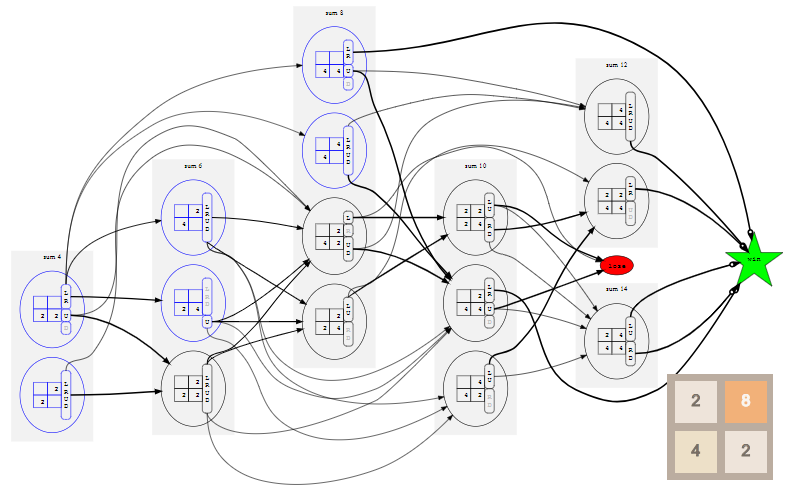
Случайное начальное число (random seed) определяет случайную последовательность тайлов, добавляемых игрой на поле. «Стратегия» игрока задаётся таблицей, называемой алгоритмом (policy). Она сообщает нам, в каком направлении нужно сдвигать тайлы в любой возможной конфигурации поля. В этом посте мы рассмотрим способ создания алгоритма, оптимального в том смысле, что он максимизирует шансы игрока на получение тайла 32.

Оказывается, что в игре 2x2 до тайла 32 очень сложно выиграть — даже если играть оптимально, игрок выигрывает только примерно в 8% случаев, то есть игра оказывается не особо интересной. Качественно игры 2x2 сильно отличаются от игр 4x4, но они всё равно полезны для знакомства с основными принципами.

В идеале мы хотим найти оптимальный алгоритм для полной игры на поле 4x4 до тайла 2048, но как мы убедились из предыдущего поста, количество возможных конфигураций поля очень велико. Поэтому невозможно создать оптимальный алгоритм для полной игры, по крайней мере, с помощью используемых здесь методов.

Однако мы можем найти оптимальный алгоритм для укороченной игры 4x4 до тайла 64, и, к счастью, мы увидим, что оптимальная игра на полях 3x3 качественно выглядит похожей на некоторые успешные стратегии полной игры.

Код (исследовательского качества), на котором основана эта статья, выложен в открытый доступ.
Читать полностью »