
Рубрика «тождество эйлера»
Эйлер, Чёрч и Мандельброт — этюд о красоте и математике
2023-07-18 в 17:17, admin, рубрики: кодирование чёрча, Колмогоров, красота, лямбда-исчисление, математика, множество мандельброта, Научно-популярное, тождество эйлера, Читальный зал
Самая красивая теорема математики: тождество Эйлера
2019-05-31 в 7:20, admin, рубрики: кватернионы, комплексные числа, математика, Научно-популярное, тождество эйлера, тригонометрия, число пиПосмотрев лекцию профессора Робина Уилсона о тождестве Эйлера, я наконец смог понять, почему тождество Эйлера является самым красивым уравнением. Чтобы поделиться моим восхищением это темой и укрепить собственные знания, я изложу заметки, сделанные во время лекции. А здесь вы можете купить его прекрасную книгу.
Что может быть более загадочным, чем взаимодействие мнимых чисел с вещественными, в результате дающее ничто? Такой вопрос задал читатель журнала Physics World в 2004 году, чтобы подчеркнуть красоту уравнения Эйлера «e в степени i, умноженного на пи равно минус единице».
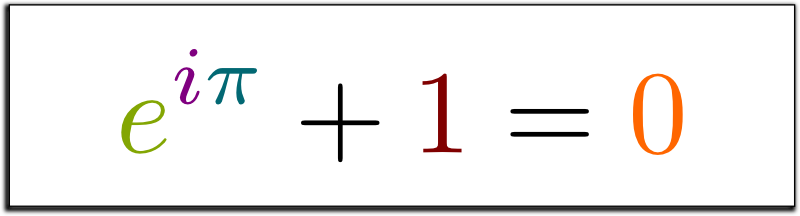
Рисунок 1.0: тождество Эйлера — e в степени i, умноженного на пи, плюс единица равно нулю.
Ещё раньше, в 1988 году, математик Дэвид Уэллс, писавший статьи для американского математического журнала The Mathematical Intelligencer, составил список из 24 теорем математики и провёл опрос, попросив читателей своей статьи выбрать самую красивую теорему. И после того, как с большим отрывом в нём выиграло уравнение Эйлера, оно получило званием «самого красивого уравнения в математике».
Читать полностью »
