Привет! Я очень долго собирался с мыслями, чтобы попробовать опубликовать свою статью в вашем сообществе, это дебют, поэтому буду рад услышать в комментариях обратную связь по поводу содержимого материала. Тематика сегодняшнего сообщения – это разбор базовых понятий в теории вероятностей с помощью языка программирования Python.
Рубрика «теория вероятностей» - 3
Основы теории вероятностей с помощью Python
2022-03-04 в 16:00, admin, рубрики: python, математика, начало анализа данны, понятие вероятности, Программирование, Профессиональная литература, Статистика в IT, теория вероятностей, учебная задачаКвантовая теория. Вселенная из волн вероятностей
2020-10-18 в 0:11, admin, рубрики: квантовая физика, квантовые алгоритмы, Научно-популярное, теория вероятностейКвантовая теория является одной из самых точных моделей, описывающих окружающий нас мир, а технические решения, разработанные благодаря применению аппарата квантовой механики, прочно вошли в повседневную жизнь современного общества. И тем удивительнее, что понимание даже базовых концепций этой сферы знаний вступает в серьезные противоречия с интуицией, не только людей далеких от науки, но и самих исследователей, подтверждением чему является большое количество различных интерпретаций. В этой статье, предлагаю рассмотреть основные понятия квантовой теории с показавшейся автору наиболее интуитивно-понятной точки зрения, несколько модифицированной теории вероятностей.
 Что будет, если по аналогии с двущелевым опытом, все пространство на пути частицы до экрана будет заполнено щелями?
Что будет, если по аналогии с двущелевым опытом, все пространство на пути частицы до экрана будет заполнено щелями?
Байесовские сети при помощи Питона — что и зачем?
2020-07-11 в 5:52, admin, рубрики: data mining, Анализ и проектирование систем, Научно-популярное, перевод, теория вероятностейДисклеймер: данная статья является адаптированным переводом. Оригинал можно прочесть здесь.
Байесовские сети при помощи Питона — объяснение с примерами
Из-за ограниченности информации (особенно на родном русском) и ресурсов работы, байесовские сети окружены рядом проблем. И можно было бы спать спокойно, если бы их реализация не осуществлялась в большинстве передовых технологий эры, таких как искусственный интеллект и машинное обучение.
Основываясь на данном факте, эта статья полностью посвящена работе Байесовских сетей и тому, как они сами могут не формировать проблемы, а применяться в их решении, даже если решаемые проблемы крайне запутаны.
Читать полностью »
Визуальная теория информации (часть 2)
2020-01-21 в 19:40, admin, рубрики: кодирование, математика, математическая статистика, машинное обучение, сжатие, Статистика в IT, теория вероятностей, теория информации, энтропия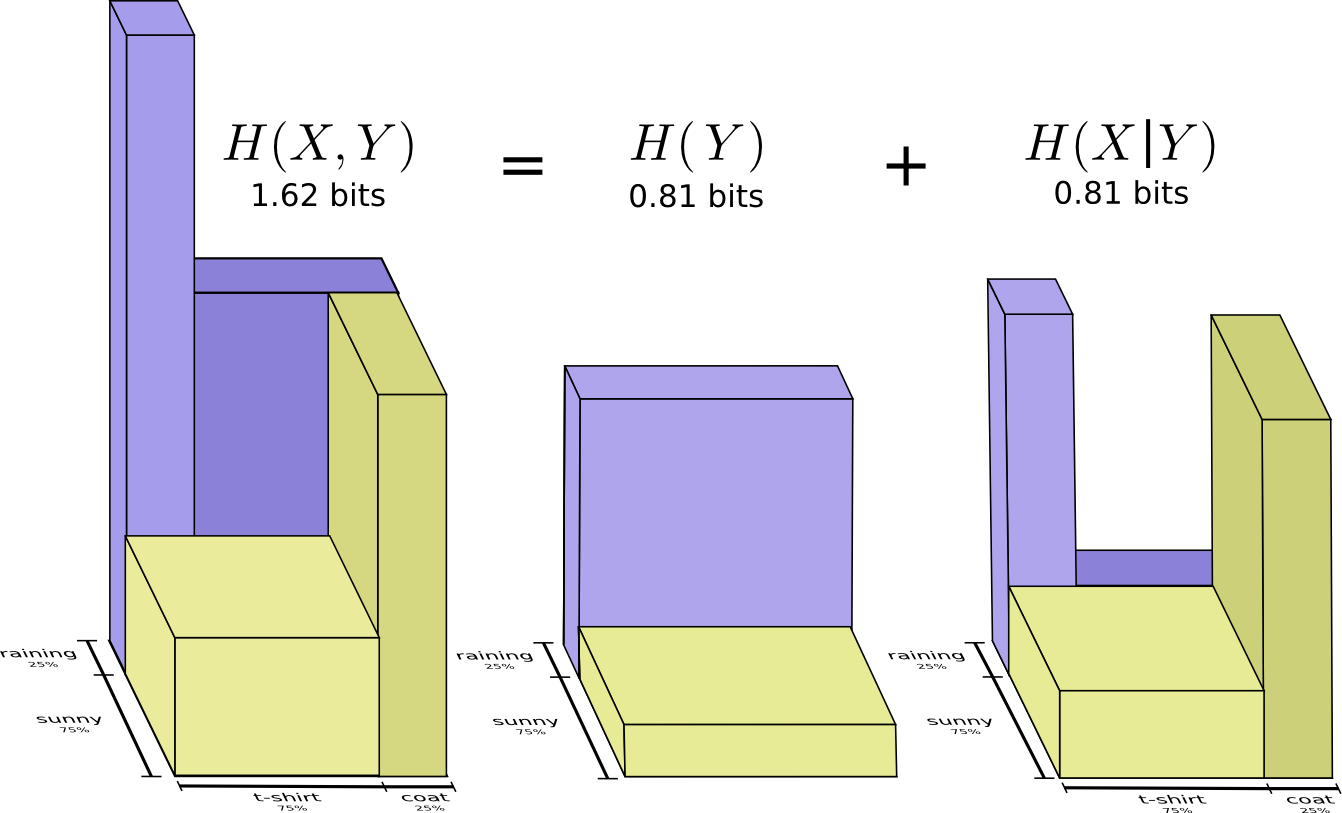
Вторая часть перевода лонгрида посвященного визуализации концепций из теории информации. Во второй части рассматриваются энтропия, перекрестная энтропия, дивергенция Кульбака-Лейблера, взаимная информация и дробные биты. Все концепции снабжены прекрасными визуальными объяснениями.
Для полноты восприятия, перед чтением второй части, рекомендую ознакомиться с первой.
Визуальная теория информации (часть 1)
2020-01-20 в 14:09, admin, рубрики: кодирование, математика, математическая статистика, машинное обучение, сжатие, Статистика в IT, теория вероятностей, теория информации, энтропия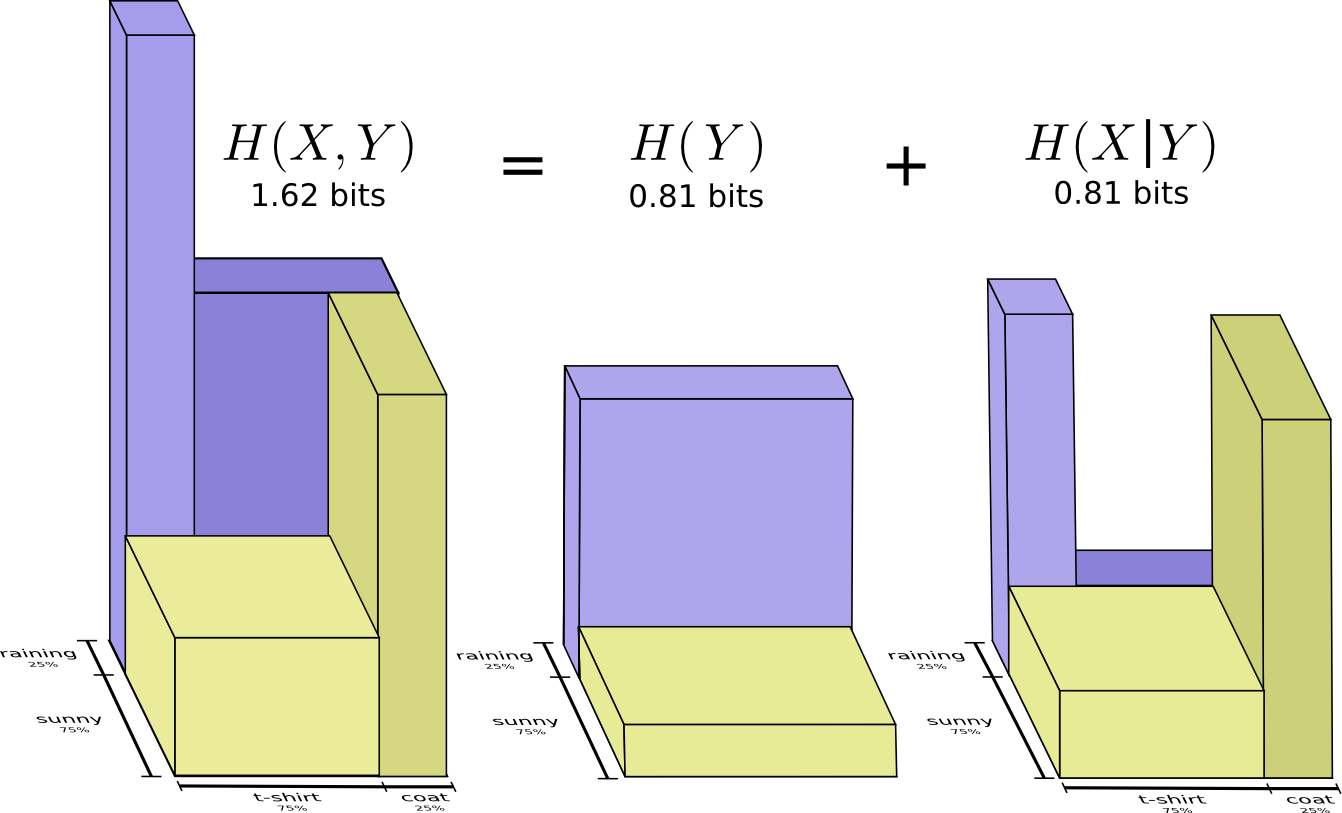
Перевод интересного лонгрида посвященного визуализации концепций из теории информации. В первой части мы посмотрим как отобразить графически вероятностные распределения, их взаимодействие и условные вероятности. Далее разберемся с кодами фиксированной и переменной длины, посмотрим как строится оптимальный код и почему он такой. В качестве дополнения визуально разбирается статистический парадокс Симпсона.
Теория информации дает нам точный язык для описания многих вещей. Сколько во мне неопределенности? Как много знание ответа на вопрос А говорит мне об ответе на вопрос Б? Насколько похож один набор убеждений на другой? У меня были неформальные версии этих идей, когда я был маленьким ребенком, но теория информации кристаллизует их в точные, сильные идеи. Эти идеи имеют огромное разнообразие применений, от сжатия данных до квантовой физики, машинного обучения и обширных областей между ними.
К сожалению, теория информации может казаться пугающей. Я не думаю, что есть какая-то причина для этого. Фактически, многие ключевые идеи могут быть объяснены визуально!
Гидрология и математика редких событий, или Неоспоримый аргумент в пользу выживальщиков
2019-11-29 в 9:47, admin, рубрики: выживание, математика, Научно-популярное, оценка рисков, перевод, планирование, теория вероятностейПривет! Представляю вашему вниманию перевод статьи «The Surprisingly Solid Mathematical Case of the Tin Foil Hat Gun Prepper» автора BJ Campbell.
«Всего лишь девять приемов пищи отделяют человечество от анархии», – Альфред Генри Льюис, 1906 год.
Конспект по «Машинному обучению». Теория вероятностей. Формула Байеса
2019-11-03 в 20:05, admin, рубрики: вероятность, искусственный интеллект, конспект, математика, машинное обучение, нейросети, теория вероятностей, условная вероятность, формула Байеса
Теория вероятностей. Формула Байеса
Пусть проводится некоторый эксперимент.


Читать полностью »
Математическое обоснование нецелесообразности бежать вниз по эскалатору в метро
2019-10-26 в 17:45, admin, рубрики: математика, теория вероятностей, теория игрВопреки правилам пользования метрополитеном, желая сэкономить время, каждый из нас хотя бы раз в жизни бежал вниз по эскалатору. На первый взгляд кажется, что это абсолютно логично и правильно: хочешь быстрее уехать – постарайся оказаться на платформе как можно раньше. Однако, практически сразу в голову приходит следующий сценарий: вы сломя голову летите по эскалатору вниз, спускаетесь на платформу, а двери вагона закрываются прямо перед вашим носом. Пока вы ждёте следующий поезд – люди, которые вставали на эскалатор одновременно с вами, успевают стоя на месте спокойно спуститься и сесть в следующий поезд. В таком случае – выигрыша никакого. Так насколько же рационально бежать по эскалатору вниз и стоит ли заниматься этим вообще? Спешу вас обрадовать – ответ найден! Ниже представлено математическое обоснование нецелесообразности (да, именно НЕ) бежать вниз по эскалатору в метро.
Читать полностью »
Исследуем утверждение центральной предельной теоремы с помощью экспоненциального распределения
2019-10-11 в 20:52, admin, рубрики: python, математика, математическая статистика, теория вероятностейВместо введения
В статье описывается исследование, проведенное с целью проверки утверждения центральной предельной теоремы о том, что сумма N независимых и одинаково распределенных случайных величин, отобранных практически из любого распределения, имеет распределение, близкое к нормальному. Однако, прежде чем мы перейдем к описанию исследования и более подробному раскрытию смысла центральной предельной теоремы, не лишним будет сообщить, зачем вообще проводилось исследование и кому может быть полезна статья.
В первую очередь, статья может быть полезна всем начинающим постигать основы машинного обучения, в особенности если уважаемый читатель еще и на первом курсе специализации «Машинное обучение и анализ данных». Именно подобного рода исследование требуется провести на заключительной неделе первого курса, указанной выше специализации, чтобы получить заветный сертификат.
Читать полностью »
Неслучайный генератор случайных одноразовых кодов Тинькофф банка
2019-07-31 в 15:40, admin, рубрики: информационная безопасность, теория вероятностей, тинькофф банкСовершая очередную транзакцию в моем любимом банке Тинькофф, получил уже привычное сообщение:
Никому не говорите код: 3131! Перевод с карты ****. Сумма ***.00 RUB
Если будут спрашивать — я вам его не говорил.
И снова взгляд зацепился за интересное совпадение цифр в «случайном» одноразовом коде (вспомнился Нео с чёрной кошкой). В итоге решил поднять всю историю сообщений, чтобы посмотреть, насколько случаен «случайный» одноразовый код и чем это может грозить.

