Привет, меня зовут Марат Зимнуров и я тимлид в кросс-функциональной команде HR Admin Tech Авито. Наверняка, вы уже сталкивались с термином «функциональное программирование» (ФП). Если посмотреть на популярные доклады (например, на HolyJS), тема функционального программирования раскрыта довольно поверхностно: immutable-структуры, transitions — и всё. В русскоязычном сегменте нет нормального baseline-гайда, с которого можно начать, да и в англоязычном ситуация не лучше: пара разрозненных курсов и несколько докладов про иммутабельность и монады от хаскелиста.
Рубрика «теория категорий»
От Аристотеля до Тьюринга: что такое функциональное программирование и как оно облегчает жизнь
2025-07-11 в 14:17, admin, рубрики: ненормальное программирование, теория, теория категорий, философия программирования, философия разработки, функциональное программирование, функциональщинаЯзык мироздания — теория групп и теория категорий
2025-04-21 в 10:07, admin, рубрики: галуа, монада, теория групп, теория категорий, функтор
Около полутора лет назад я опубликовал на Хабре статью под названием "Слово Божие — функциональное программирование как основа ВселеннойЧитать полностью »
Монады с точки зрения программистов (и немного теории категорий)
2019-03-27 в 15:19, admin, рубрики: haskell, математика, монады, Программирование, теория категорий, теория категорий для программистов, функциональное программированиеВведение
Как узнать, что человек понял, что такое монады? Он сам вам об этом расскажет в первые 5 минут общения и обязательно попробует объяснить. А ещё напишет об этом текст и по возможности где-нибудь его опубликует, чтобы все остальные тоже поняли, что такое монады.
Среди функциональных программистов, особенно на Haskell, монады стали чем-то вроде локального мема. Их часто пытаются объяснить, отталкиваясь от частных случаев и сразу приводя примеры использования. Из-за этого слушатель может не уловить основную суть понятия, а монады так и останутся чёрной магией, ну или просто средством костылизации побочных эффектов в чисто функциональных языках.
Я сначала расскажу про базовые понятия теории категорий, а затем мы с практической точки зрения подойдём к определению монады и увидим, что на самом деле очень многие программисты пользуются этой мощной абстракцией в одном из её проявлений.
Моё изложение во многом основывается на книге Бартоша Милевски "Теория категорий для программистов", которая создавалась как серия блогпостов, доступна в PDF, а недавно вышла в бумаге.
Примеры приводятся на Haskell, предполагается, что читатель знаком с синтаксисом и основными понятиями языка. В упомянутой книге есть примеры и на С++, можете сравнить чистоту и понятность кода.

Типизируя техническое интервью
2017-05-03 в 14:29, admin, рубрики: aphyr, haskell, Алгоритмы, перевод с английского, прекрасное, теория категорий, функциональное программирование, чёрная магия, метки: aphyrПредлагаю читателям "Хабрахабра" перевод статьи Kyle Kingsbury, a.k.a "Aphyr".
Ранее: Заклиная техническое интервью
В прежние времена, задолго до восхода Церкви, все заклятья произносились по чистому случаю, все действия были разрешены, а смерть была обыденностью. Многие ведьмы покалечились из-за своей магии, их находили изломанными в центре круга искривленных, застеклившихся деревьев и горящих камней, не гаснущих даже под водой; некоторые полностью исчезали, или начинали путешествовать по горным перевалам, никогда не касаясь ногами земли, никогда не согревая воздух своим дыханием.
Теория категорий на JavaScript. Часть 1. Категория множеств
2016-10-31 в 2:29, admin, рубрики: d3.js, javascript, Блог компании Группа компаний «ЦИТ» (Центр ИТ), математика, ооп, теория категорий, функциональное программирование
Абстракция – это одна из основных техник в ИТ. Любой язык программирования или моделирования, любая парадигма программирования (процедурная, функциональная, ООП, …) дают ответ на вопрос, как и от чего нужно абстрагироваться. Причём, адепты каждого подхода предлагают какой-то свой вариант абстракции.
Если вы хотите увидеть истинную, универсальную абстракцию, то вступайте в нашу… изучайте теорию категорий. В статье на примере категории множеств с картинками и JavaScript-кодом объясняются самые базовые понятия теории категорий: пределы, универсальное свойство. Рассматривается вычислительный аспект теории категорий.
Также немного говорится про классы, примеси и смеси в JavaScript.
Примеры из статьи можно посмотреть тут.
Читать полностью »
Функторы (глава книги «Теория категорий для программистов»)
2016-07-07 в 7:32, admin, рубрики: c++, fmap, haskell, list, maybe, reader, математика, теория категорий, теория категорий для программистов, функторы, функциональное программирование, метки: теория категорий, теория категорий для программистов, функторыЭто седьмая статья из цикла «Теория категорий для программистов». Предыдущие статьи уже публиковались на Хабре:
- Теория категорий для программистов: предисловие
- Категория: суть композиции
- Типы и функции
- Категории, большие и малые
- Категории Клейсли
- Произведения и копроизведения
- Простые алгебраические типы данных
Функторы
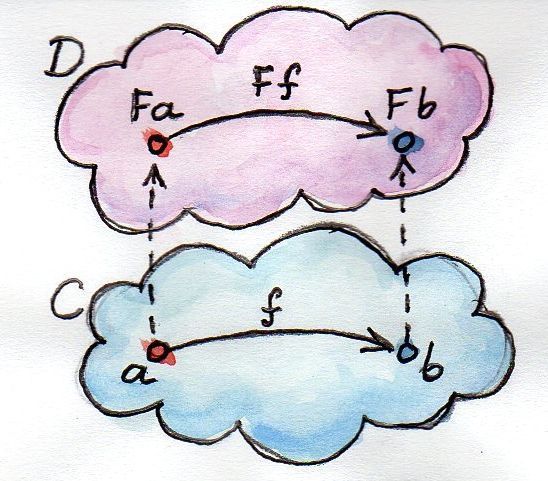
За понятием функтора стоит очень простая, но мощная идея (как бы заезжено это ни прозвучало). Просто теория категорий полна простых и мощных идей. Функтор есть отображение между категориями. Пусть даны две категории C и D, а функтор F отображает объекты из C в объекты из D — это функция над объектами. Если a — это объект из C, то будем обозначать его образ из D как F a (без скобок). Но ведь категория — это не только объекты, но еще и соединяющие их морфизмы. Функтор также отображает и морфизмы — это функция над морфизмами. Но морфизмы отображаются не как попало, а так, чтобы сохранять связи. А именно, если морфизм f из C связывает объект a с объектом b,
f :: a -> bто образ f в D, F f, связывает образ a с образом b:
F f :: F a -> F b(Надеемся, что такая смесь математических обозначений и синтаксиса Haskell понятна читателю. Мы не будем писать скобки, применяя функторы к объектам или морфизмам.)
Категории Клейсли
2015-01-28 в 14:12, admin, рубрики: c++, haskell, математика, Программирование, теория категорий, функциональное программированиеКомпозиция логирования
Вы видели, как сделать категорию типов и чистых функций. Я также упомянул, что есть способ смоделировать побочные эффекты, или нечистые функции, в рамках теории категорий. Давайте рассмотрим пример: функции, которые логируют или записывают ход своего выполнения.
Читать полностью »
Категории, большие и малые
2015-01-19 в 13:29, admin, рубрики: c++, haskell, математика, Программирование, теория категорий, функциональное программированиеЭто четвертая статья в цикле «Теория категорий для программистов».
Понять пользу категорий можно изучая различные примеры. Категории бывают всех форм и размеров и часто появляются в самых неожиданных местах. Мы начнем с самых простых.
Без объектов
Самая простая категория — без объектов и, как следствие, без морфизмов. Читать полностью »
Типы и функции
2015-01-13 в 8:51, admin, рубрики: c++, haskell, математика, Программирование, теория категорий, функциональное программированиеЭто третья статья в цикле «Теория категорий для программистов».
Категория типов и функций играет важную роль в программировании, так что давайте поговорим о том, что такое типы, и зачем они нам нужны.
Кому нужны типы?
В сообществе есть некоторое несогласие о преимуществах статической типизации против динамической и сильной типизации против слабой. Позвольте мне проиллюстрировать выбор типизации с помощью мысленного эксперимента. Представьте себе миллионы обезьян с клавиатурами, радостно жмущих случайные клавиши, которые пишут, компилируют и запускают программы.

Святая Троица
2015-01-04 в 10:41, admin, рубрики: логика, математика, соответствие Карри-Ховарда, теория категорий, теория типов, функциональное программированиеХристианское учение о Троице — это представление о едином Боге, выступающем в ипостасях Бога-Отца, Бога-Сына и Святого Духа. Доктрина вычислительного тринитаризма состоит в том, что вычисление представляется в трех формах: доказательствах высказываний, программах некоторого типа и отображений между структурами. Каждый из этих аспектов есть объект поклонения одной из трех деноминаций: логики, утверждающей главенство доказательств и высказываний, теории языков программирования, обращающейся в первую очередь к программам и типам, и теории категорий, отдающей первенство отображениям и структурам. Основной догмат вычислительного тринитаризма гласит, что логики, языки программирования и категории — всего лишь манифестации единого божественного понятия вычисления. Не существует наилучшего пути к просветлению, каждый из аспектов даёт возможность понимания того, что в нашей жизни представляет собой опыт вычисления.