Рубрика «теория графов»

в 18:12, , рубрики: Алгоритмы, веса, граф, графики, графы, искусственный интеллект, массив, математика, матрица, машинное обучение, петли, ребра графа, Сетевые технологии, списки, теория графов

Все, что познается, имеет число, ибо невозможно ни понять ничего, ни познать без него – Пифагор

В этой статье:

Матрица смежности

Матрица инцидентности

Список смежности (инцидентности)

Взвешенный граф (коротко)

Итак, мы умеем задавать граф графическим способом. Но есть еще два способа как можно задавать граф, а точнее представлять его. Для экономии памяти в компьютере граф можно представлять с помощью матриц или с помощью списков.

Матрица является удобной для представления плотных графов в которых количество ребер (E) примерно равно количеству вершин (V).

Читать полностью »

в 11:27, , рубрики: графы, математика, Научно-популярное, планарные графы, теория графов

Два специалиста по информатике нашли в весьма неожиданном месте идею, которая как раз пригодилась им для прорыва в теории графов

Новый алгоритм проверки пересечений в графах прятался на виду - 1

В октябре 2019 Джейкоб Холм и Ева Ротенберг пролистывали работу, опубликованную ими за несколько месяцев до этого – и вдруг поняли, что наткнулись на нечто серьёзное.

Десятилетиями специалисты по информатике пытались разработать быстрый алгоритм для определения того, можно ли добавить к определённому графу рёбра так, чтобы он остался «планарным» – то есть, чтобы его рёбра не пересекались. Однако ни у кого не получалось улучшить алгоритм, опубликованный более 20 лет назад.

Холм и Ротенберг с удивлением обнаружили, что в их работе есть идея, позволявшая достаточно сильно улучшить этот алгоритм. Она «разобралась с одним из главных препятствий на пути к реальному алгоритму», — сказал Холм, специалист по информатике из Копенгагенского университета. «Возможно, мы полностью раскрыли этот вопрос».
Читать полностью »

в 7:00, , рубрики: дерево, математика, Научно-популярное, полный граф, теория графов

Математики доказали, что копиями графов меньшего размера всегда можно идеально покрыть графы большего размера

8 января трое математиков опубликовали доказательство теоремы из комбинаторики, сформулированной почти 60 лет назад, известной, как гипотеза Рингеля. Грубо говоря, она предсказывает, что графы – конструкции, состоящие из точек и линий – можно идеально сложить из одинаковых частей меньшего размера.

Математики с восторгом приняли подтверждение этой гипотезы.

«Счастье в том, что эта работа решает очень старую гипотезу, которую невозможно было проверить другими методами», — сказал Гил Калай, математик из Еврейского университета в Иерусалиме, не связанный с этой работой.

Гипотеза Рингеля предсказывает, что особые типы сложных графов – с триллионами вершин и рёбер – можно «замостить», т.е. полностью покрыть, отдельными копиями меньших графов определённого типа. С концептуальной точки зрения этот вопрос похож на следующий: могу ли я полностью замостить пол на кухне одинаковыми копиями какой-либо плитки, имеющейся в магазине? В реальной жизни большинство типов плитки не подойдёт для вашей кухни – чтобы полностью покрыть пол, придётся комбинировать их разные формы. Но в мире теории графов гипотеза предсказывает, что замостить граф можно всегда.
Читать полностью »

в 15:07, , рубрики: big data, data mining, python, Алгоритмы, графы, исследование, кредитный скоринг, машинное обучение, обучение, теория графов, финансы в IT

AntipovSN and MihhaCF

Часть вторая, в которой Атосу все норм, а вот Графу де ля Фер чего-то не хватает

Вступление от авторов:

Добрый день! Сегодня мы продолжаем цикл статей, посвященный скорингу и использованию в оном теории графов. С первой статьей Вы можете ознакомиться здесь.

Все шуточные аллегории, вставки и прочее призваны немного разгрузить повествование и не позволить ему свалиться в нудную лекцию. Всем, кому не зайдет наш юмор, заранее приносим извинения

Цель данной статьи: не более, чем за 30 минут, описать основные способы хранения данных о графах и описать правила и принципы построения нашей модели для скоринга заемщика.

Термины и определения:

  • Хеш-таблица — это структура данных, реализующая интерфейс ассоциативного массива, она позволяет хранить пары (ключ, значение) и выполнять три операции: операцию добавления новой пары, операцию поиска и операцию удаления пары по ключу. Поиск по хеш-таблице, в среднем, осуществляется за время О(1).

Аудиторы, нанятые ПАО «Король» для оценки кредитоспособности НПАО «Один за всех», столкнулись с некоторыми проблемами. С одной стороны, описать схему взаимодействия 10-15 компаний и провести первичную оценку взаимодействия между компаниями очень просто, достаточно иметь под рукой лист бумаги и ручку. Но, что делать, если у вас имеется информация о взаимодействии десятков или сотен тысяч компаний? Например, если Вам нужно описать взаимодействия Арамиса со всеми его пассиями или Д’артаньяна со всеми, с кем он дрался?

Читать полностью »

в 16:51, , рубрики: big data, data mining, python, Алгоритмы, графы, исследование, кредитный скоринг, машинное обучение, обучение, теория графов, финансы в IT

AntipovSN and MihhaCF

Часть первая, в которой Граф еще не стал Атосом, не встретил Миледи и все у него хорошо

Вступление от авторов:

Добрый день! Сегодня мы начинаем цикл статей, посвященных скорингу и использованию в оном теории графов (Т.Г.). Надеюсь, нам хватит запала, сил и терпения, т.к. тема достаточно объемная и, на наш взгляд, интересная.

Несмотря на шуточное название, мы постараемся затронуть отнюдь не шуточные темы, которые уже сейчас влияют на жизнь многих из нас, а в ближайшем будущем могут коснуться всех, без исключения.

Все шуточные аллегории, вставки и прочее призваны немного разгрузить повествование и не позволить ему свалиться в нудную лекцию. Всем, кому не зайдет наш юмор, заранее приносим извинения

А теперь к делу.

Цель данной статьи: не более, чем за 30 минут, ввести читателя в проблематику исследования, определить уровень рассмотрения проблемы, описать основную концепцию исследования и познакомить с базовыми терминами.

Термины и определения:

  • Скоринг – система бальной оценки объекта, основанная на численных статистических методах.
  • Граф – способ моделирования связей объектов. Представьте, что Вы с друзьями играете в покер и хотите смоделировать, кто кому сейчас должен. Например, «Д’Артаньян должен Атосу 10 луидоров»

Граф Скоринг де ля Фер или исследование на тему кредитного скоринга, в рамках расширения кругозора - 1

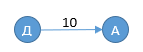
Полный граф может выглядеть следующим образом:
Граф Скоринг де ля Фер или исследование на тему кредитного скоринга, в рамках расширения кругозора - 2
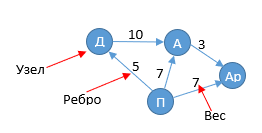
Арамис всегда был хитрож… себе на уме, ему должен даже Атос. Портос, пока не встретил госпожу Кокнар, перевязь не мог себе нормальную купить и умудрился задолжать нищеброду Д’артаньяну, хотя, честно говоря, они всю дорогу что-то мутили вместе…

Читать полностью »

в 7:00, , рубрики: гипотеза Хедетниеми, графы, математика, Научно-популярное, теория графов, хроматические числа

Всего три страницы потребовалось российскому математику, чтобы описать способ раскраски сетей определённого типа, превзошедший ожидания экспертов

Российский математик опроверг 53-летнюю гипотезу о раскраске сетей - 1

В опубликованной в онлайне работе опровергается гипотеза 53-летней давности, касающаяся наилучшего способа назначения цветов узлам сети. В работе всего на трёх страничках показано существование способов раскраски определённых цветов, превзошедших все ожидания экспертов.

Задачи по раскраске сетей [см. хроматическое число / прим. перев.], вдохновлённые вопросом такой раскраски карт, при которой соседние страны имеют разные цвета, находятся в фокусе исследований математиков почти 200 лет. Задача состоит в том, чтобы понять, как раскрашивать узлы некоей сети (или графа, как зовут их математики) так, чтобы у любых двух связанных узлов были разные цвета. В зависимости от контекста, эта раскраска может предоставить эффективный способ рассадки гостей на свадьбе, расстановке производственных задач по свободным временным промежуткам, или даже решения судоку.
Читать полностью »

в 9:00, , рубрики: Алгоритмы, математика, поиск, поиск ближайшего соседа, сортировка, теория графов

Обнаружен универсальный метод сортировки сложной информации - 1

Открывая своё кафе, вы хотели бы узнать ответ на следующий вопрос: «где находится другое, ближайшее к этой точке кафе?» Эта информация помогла бы вам лучше понять ваших конкурентов.

Это пример задачи поиска "ближайшего соседа", которую широко изучают в информатике. Дан набор сведений и новая точка, и требуется найти, к какой точке из уже существующих она окажется ближайшей? Такой вопрос возникает во множестве повседневных ситуаций в таких областях, как исследование генома, поиск картинок и рекомендации на Spotify.

Но, в отличие от примера с кафе, вопросы о ближайшем соседе часто оказываются очень сложными. За последние несколько десятилетий величайшие умы среди специалистов по информатике брались за поиски наилучших способов решения подобной задачи. В частности, они пытались справиться с усложнениями, появляющимися из-за того, что в различных наборах данных могут быть очень разные определения «близости» точек друг к другу.
Читать полностью »

в 8:53, , рубрики: искусственный интеллект, математика, модель памяти, Научно-популярное, нейронные сети, симуляция мозга, теория графов
image

Сегодня утром на пути к кампусу Беркли я провёл пальцами по листьям ароматного куста, а затем вдохнул знакомый запах. Я делаю так каждый день, и каждый день первое слово, которое всплывает в голове и приветственно машет рукой — это шалфей (sage). Но я знаю, что это растение — не шалфей, а розмарин, поэтому я приказываю шалфею успокоиться. Но слишком поздно. После rosemary и sage я не могу помешать появлению на сцене петрушки (parsley) и чабреца (thyme), после чего в голове возникают первые ноты мелодии и лица на обложке альбома, и вот я уже снова оказался в середине 1960-х, одетый в рубашку с огурцами. Тем временем розмарин (rosemary) вызывает в памяти Роуз Мэри Вудс (Rosemary Woods) и 13-минутный пробел (хотя теперь, проконсультировавшись с коллективной памятью, я знаю, что это должны быть Роуз Мэри Вудс и пробел в 18 с половиной минут). От Уотергейта я перепрыгиваю к историям на главной странице. Потом я замечаю в ухоженном саду ещё одно растение с пушистыми серо-зелёными листями. Это тоже не шалфей, а чистец (lamb’s ear). Тем не менее, sage наконец получает свою минуту славы. От трав я переношусь к математическому ПО Sage, а потом к системе противовоздушной обороны 1950-х под названием SAGE, Semi-Automatic Ground Environment, которой управлял самый крупный из когда-либо построенных компьютеров.

В психологии и литературе подобные мыслительные блуждания называются потоком сознания (автор этой метафоры — Уильям Джеймс). Но я бы выбрал другую метафору. Моё сознание, насколько я ощущаю, не течёт плавно от одной темы к другой, а скорее порхает по ландшафту мыслей, больше похожее на бабочку, чем на реку, иногда прибиваясь к одному цветку, а затем к другому, иногда уносимая порывами ветка, иногда посещающая одно и то же место снова и снова.
Читать полностью »

в 8:45, , рубрики: AI, Delphi, gpu, Алгоритмы, алгоритмы поиска, интернет, искусственный интеллект, ооп, органическая химия, поисковые технологии, Программирование, теория графов, этюды для программистов

(Этюд для программистов или заявка на Интернет-поиск нового типа)

Графы большие и маленькие: интеллектуальное решение проблемы выбора представления - 1

Программа, делающая из мухи слона (далее программа МС), показала, что неориентированный граф существительных с заданным количеством букв хоть и содержит тысячи вершин, но при этом довольно «тощий» (т.е. имеет сравнительно не много ребер) и до полного графа ему далеко (см. Пример 1). Вслед за Чарлзом Уэзереллом (Charles Wetherell), автором широко известной книги «Этюды для программистов», выбрал жанр этюда, чтобы представить различные способы представления таких графов. (И сделать из этого выводы для автоматизации выбора представления – вплоть, может быть, до Интернет-поиска нового типа).

Start for word length 8
6016 words loaded from dictionary file: ..DictionaryORF3.txt
Graph was made: edges number = 871

Пример 1. Характеристики графа существительных длиной 8 букв.
Читать полностью »

в 17:04, , рубрики: AI, Алгоритмы, головоломки, Занимательные задачки, из мухи слона, искусственный интеллект, компьютерные игры, математика, Программирование, разработка игр, теория графов

Недавно, перед тем как написать про свои соображения о путях развития ИИ, решил посмотреть, что уже писали об ИИ на Хабре. В числе прочих наткнулся на статью с довольно сложным решением (через генетический алгоритм) широко известной задачи поиска метаграмм: дано два слова (существительных) одинаковой длины, нужно получить из первого второе, меняя только одну букву и получая при этом имеющее смысл слово.

Сложно ли сделать из мухи слона? - 1
Сальвадор Дали. Искушение св. Антония. 1946. (Фрагмент).
Бельгийский Королевский музей изящных искусств (Брюссель).
Читать полностью »

123
Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js