Рубрика «теория чисел»
Математическая продлёнка. Изобретаем гиперболические числа
2024-12-01 в 18:33, admin, рубрики: гиперболические числа, двойные числа, теория представлений, теория чисел, формула БинеВ этой серии статей мы рассматриваем различные необычные виды арифметик, которые получаются из привычных числовых систем их расширением. В качестве расширения используется решение некоторого уравнения, не решаемого в исходной системе, а новая арифметика состоит из линейных комбинаций «обычных» чисел и «необычного» расширения.
Оглавление серии
Математическая продлёнка. Изобретаем эллиптические числа
2024-11-29 в 13:00, admin, рубрики: комплексные числа, мнимая единица, теория чисел, числа Гаусса, числа ЭйезенштейнаПродолжаем разбираться с числостроительством в серии заметок «Изобретаем числа». В предыдущих статьях этой серии мы последовательно подходили к построению числовых систем (алгебраических структур, которые я неформально называю арифметиками), как модулей над более простыми системами. В прошлый раз мы ввели классификацию таких арифметик, пользуясь их матричными представлениями, и разбили их на классы: эллиптические, гиперболические и параболические.
Оглавление серии
Математическая продлёнка. Изобретаем числа по-взрослому
2024-11-28 в 10:01, admin, рубрики: гауссовы числа, комплексные числа, линейность, матрицы, теория представлений, теория чиселПродолжение серии статей, в которой мы разбираемся с тем, как упорядоченная пара двух чисел способна служить моделью для различных числовых систем, как привычных, так и весьма экзотических. Первая и вторая части были посвящены построению привычных кольца целых и поля рациональных чисел, вернее тому, как эти числовые системы можно моделировать упорядоченными парами элементов из более примитивных систем.
В этой части мы рассмотрим общие принципы построения числовых систем, как модулейЧитать полностью »
Математическая продлёнка. Изобретаем дроби
2024-11-27 в 13:32, admin, рубрики: рациональные дроби, теория чисел, факторизация, эквивалентные классыЭто вторая часть серии статей, посвящённой построению числовых систем, основанных на упорядоченных парах (целые, рациональные, гауссовы, двойные, дуальные...). В предыдущей статье мы рассмотрели как строится кольцо целых чисел из пары натуральных, освоившись с понятиями классов эквивалентности и факторизацией. В этой построим ещё одну знакомую числовую систему: поле рациональных чисел.
Математическая продлёнка. Изобретаем целые числа
2024-11-26 в 19:23, admin, рубрики: теория представлений, теория чисел, факторизация, целые числа, эквивалентные классыВ этой мини-серии статей я хочу объединить свои заметки для математического кружка о различных необычных, но полезных числовых системах, основанных на парах чисел. План знакомства с числовыми системами будет такой:
-
В этой статье мы (признаюсь, достаточно занудно) построим из натуральных чисел целые, при этом познакомимся с важнейшими инструментами математики: упорядоченной парой, эквивалентностью и факторизацией.
-
Во второй части от целых мы перейдём к рациональным числам, которые тоже можно представить в виде пары — Читать полностью »
Молодые математики открывают новую главу в изучении простых чисел
2023-11-05 в 10:00, admin, рубрики: ruvds_перевод, математика, теория чисел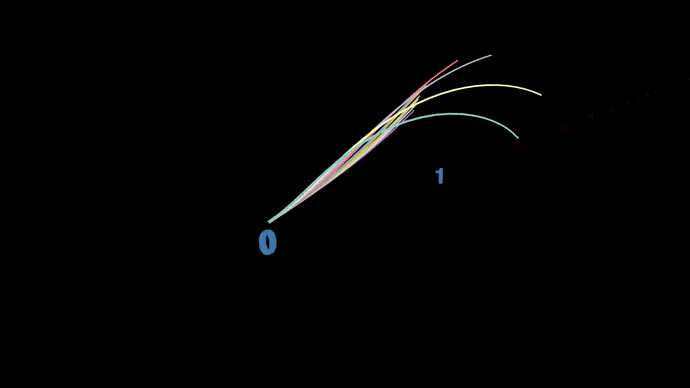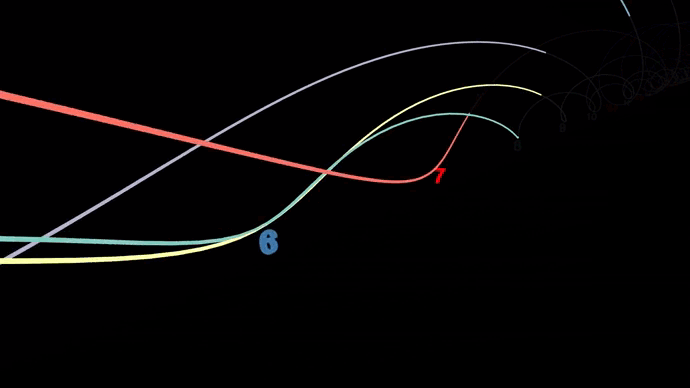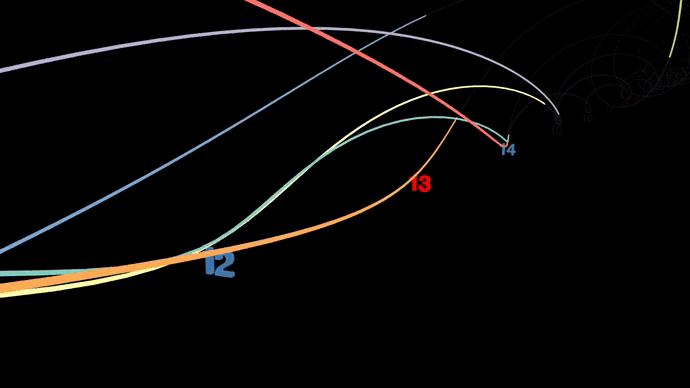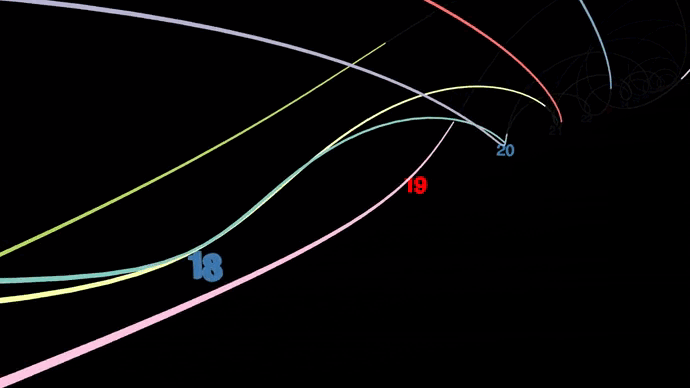
Анимация отсева по Эратосфену, где показаны кратные величины каждого простого числа, простирающиеся вдоль числовой оси.
Более 2,000 лет назад греческий математик Эратосфен разработал метод поиска простых чисел, получивший название решето Эратосфена, который остаётся актуальным по сей день. Его идея заключалась в том, чтобы определять простые числа вплоть до заданной точки путём постепенного «отсеивания» тех, которые таковыми не являются. Начинается отсев с вычёркивания всех чисел, кратных 2 (кроме самой 2), затем кратных 3 (кроме 3). Следующее число, 4, уже оказывается вычеркнуто, значит, очередным шагом идёт вычёркивание всех чисел, кратных 5 и так далее. Все оставшиеся в итоге числа считаются простыми, то есть такими, которые делятся только на 1 и на самих себя.
Эратосфен работал со всем множеством простых чисел, но вы можете использовать вариации его метода для поиска таких, которые будут обладать особыми свойствами. Хотите найти «близнецов», которые отличаются всего на 2 единицы, например, 11 и 13 или 599 и 601? Для этого есть свой отсев. Интересуют простые числа, которые на 1 больше полного квадрата, например, 17 или 257? И для этого тоже есть свой отсев.Читать полностью »
Феномен постоянной Капрекара. 6174 — таинственное «число великой радости» или непреодолимая стена?
2023-10-14 в 15:24, admin, рубрики: 6174, вычисления, занимательные задачи, Занимательные задачки, Капрекар, неподвижные точки, постоянная капрекара, теория чисел, числа харшад, число великой радостиЖара стояла невыносимая, солнце безжалостно сжигало пыльную деревенскую дорогу. Люди не могли думать ни о чём, кроме спасительной тени или живительной прохлады расположенной неподалёку реки. Среди бредущих по дороге изнурённых жарой путников выделялся один худощавый человек на велосипеде — сельский учитель, который, казалось, не замечал ни зноя, ни удушающей пыли. Он неторопливо крутил педали, а лицо его выражало радость и целеустремлённость. Да и какое ему было дело до всех невзгод, когда он размышлял о числах, об идеальном, строгом и прекрасном мире математики. В тот день его разум занимало только одно число — 6174...
Гипотеза Пойи — один из самых ярких примеров того, что в математике «верить на слово» нельзя
2023-09-06 в 15:01, admin, рубрики: гипотеза, математика, теория чиселСегодня я расскажу Вам очень показательную историю про одну математическую гипотезу из теории чисел. Она станет ярким примером того, как в математике прерываются, казалось бы, явные закономерности, и что любое предположение в этой науке нуждается в строгом доказательстве, даже если оно проверено для всех чисел, которые только могут поместиться в память суперкомпьютера.