Распределение удобное, математически выверенное. Показывает, что типичные события происходят часто, а редкие — редко. В начале двадцатого века выяснилось, что для некоторых случаев оно не подходит, более того — может выдать ложные результаты.
Например, оно не подходит для промышленного пивоварения. К такому выводу однажды пришёл учёный (и экспериментальный пивовар компании Гиннесс) Уильям Госсет. Он столкнулся с проблемой: как подойти к оценке качества сырья и продукта, если данных для анализа мало, и в итоге вывел так называемое t-распределение. У него, в отличие от распределения Гаусса, более низкий «горб» и толстые «хвосты» — края, отвечающие за маловероятные события. За счёт этих хвостов, а также благодаря своей возможности меняться, притворяясь гауссовым, t-распределение незаметно, но прочно вошло в нашу жизнь.
Правда, под именем «распределение Стьюдента».
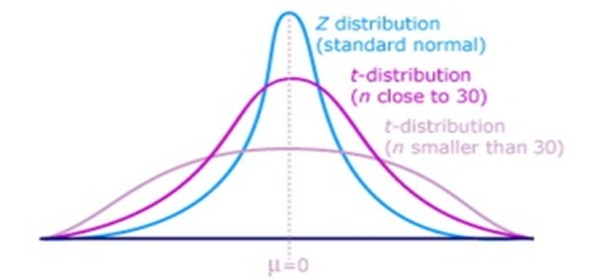
Нормальное распределение (z) и два варианта распределения Стьюдента Читать полностью »