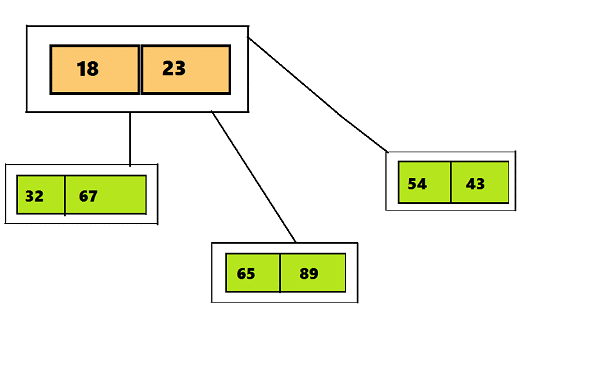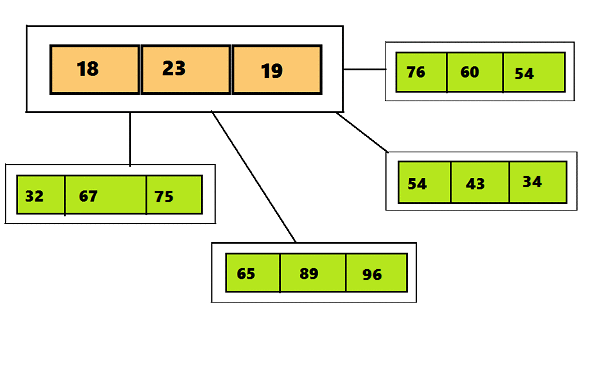
PHP имеет всего одну структуру данных для управления всем. array — сложный, гибкий, гибридный, сочетает в себе поведение list и linked map. Но мы используем его для всего, потому что PHP придерживается прагматичного подхода: иметь предельно правильный, здравый и реалистичный способ решения проблемы, исходящий из практических, а не теоретических рассуждений. array позволяет делать работу, хотя о нем и так много рассказывают на лекциях по информатике. Но, к сожалению, с гибкостью приходит и сложность.
Последний релиз PHP вызвал большое оживление в сообществе. Мы не могли дождаться того, чтобы начать использовать новые возможности и почувствовать вкус ~2х прироста производительности. Одна из причин, почему это случилось — структура array была переработана. Но массивы все также придерживаются принципа «оптимизировано для всего; оптимизировано для ничего», еще не все идеально, есть возможности для совершенствования.
А что насчет структур данных SPL?
К сожалению… они ужасны. Раньше, до PHP7, они предлагали _некоторые_ преимущества, но сейчас мы дошли до точки, когда использование SPL не имеет практического смысла.
Почему мы не можем просто поправить и улучшить их?
Да, мы могли бы, но я считаю, что их дизайн и реализация настолько бедны, что лучше бы найти более современную замену.
«SPL data structures are horribly designed.»
— Anthony Ferrara
Введение:
php-ds — расширение для PHP7, добавляющее структуры данных. Этот пост кратко охватывает поведение, производительность и преимущества каждой из них. Также в конце вы найдете список ответов на ожидаемые вопросы.
Github: https://github.com/php-ds
Пространство имен: Ds
Интерфейсы: Collection, Sequence, Hashable
Классы: Vector, Deque, Stack, Queue, PriorityQueue, Map, Set
Читать полностью »