Как известно, кривыми Безье нельзя построить дугу окружности или эллипса. В этой статье рассматриваются кривые, лишённые такого недостатка.
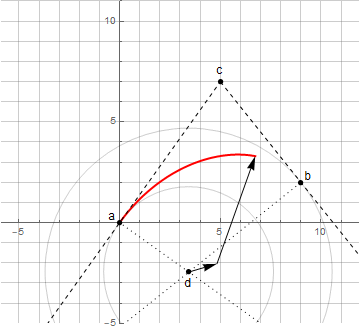
Как известно, кривыми Безье нельзя построить дугу окружности или эллипса. В этой статье рассматриваются кривые, лишённые такого недостатка.

В начале зимы Яндекс.Погода научилась показывать, будут ли осадки в ближайшие два часа. Спустя пару месяцев тема метеопрогнозирования стала центральной на одном из мероприятий Data & Science. Среди докладчиков в тот день был Алексей Преображенский — разработчик из команды Яндекс.Погоды. Алексей рассказал о нашем алгоритме наукастинга и сверточной нейросети, лежащей в основе этого алгоритма.
Под катом — расшифровка лекции и слайды.

Доброго времени!
Куча времени прошла с того момента, как я написал свою первую статью, и уже почти год с того момента, как пришла в голову идея для второй. В силу многих обстоятельств (в первую очередь – лени и забывчивости), эта идея так и не была реализована ранее, но сейчас я собрался, написал весь этот материал и готов представить его вашему вниманию.
Начну с небольшой вводной. Будучи студентом 4-го, на тот момент, курса бакалавриата, я изучал курс «Компьютерная графика». Много там было разных интересных (и не очень) заданий, но одно прямо особо запало мне в душу: интерполяция кубическими сплайнами с заданными первыми производными на концах интервала. Пользователь должен был задавать значения первых производных, а программа — считать и выводить на экран интерполяционную кривую. Особенность и основная сложность задания заключена в том, что задаются именно первые производные, а не вторые, как в классической постановке сплайн-интерполяции.
Как я ее решал, и к чему оно в итоге пришло, я как раз и изложу в этой статье. И да, если по описанию задачи вы не поняли ни в чем ее смысл, ни в чем сложность, не переживайте, все это я также постараюсь раскрыть. Итак, поехали.
А, нет, погодите один момент. Вот вам два числовых ряда:
a) 2, 4, 6, 8, ?
b) 1, 3, ?, 7, 9
Какие числа должны стоять на месте вопросов и почему? Вы действительно уверены в своем ответе?
Читать полностью »
Пусть нам дан набор точек 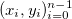 и соответствующий им набор положительных весов
и соответствующий им набор положительных весов 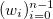 . Мы считаем, что некоторые точки могут быть важнее других (если нет, то все веса одинаковые). Неформально говоря, мы хотим, чтобы на соответствующем интервале была проведена красивая кривая таким образом, чтобы она «лучше всего» проходила через эти данные.
. Мы считаем, что некоторые точки могут быть важнее других (если нет, то все веса одинаковые). Неформально говоря, мы хотим, чтобы на соответствующем интервале была проведена красивая кривая таким образом, чтобы она «лучше всего» проходила через эти данные.
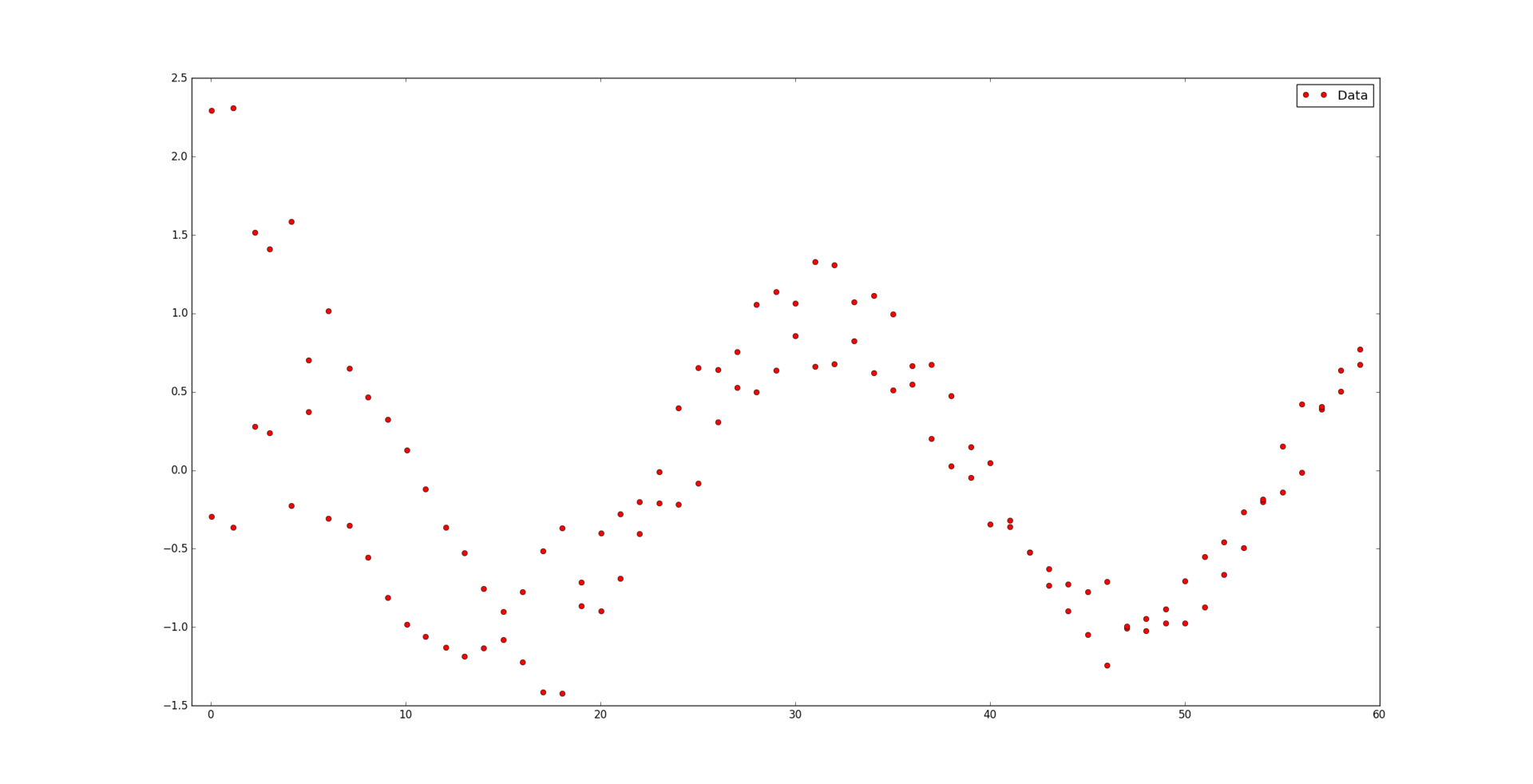
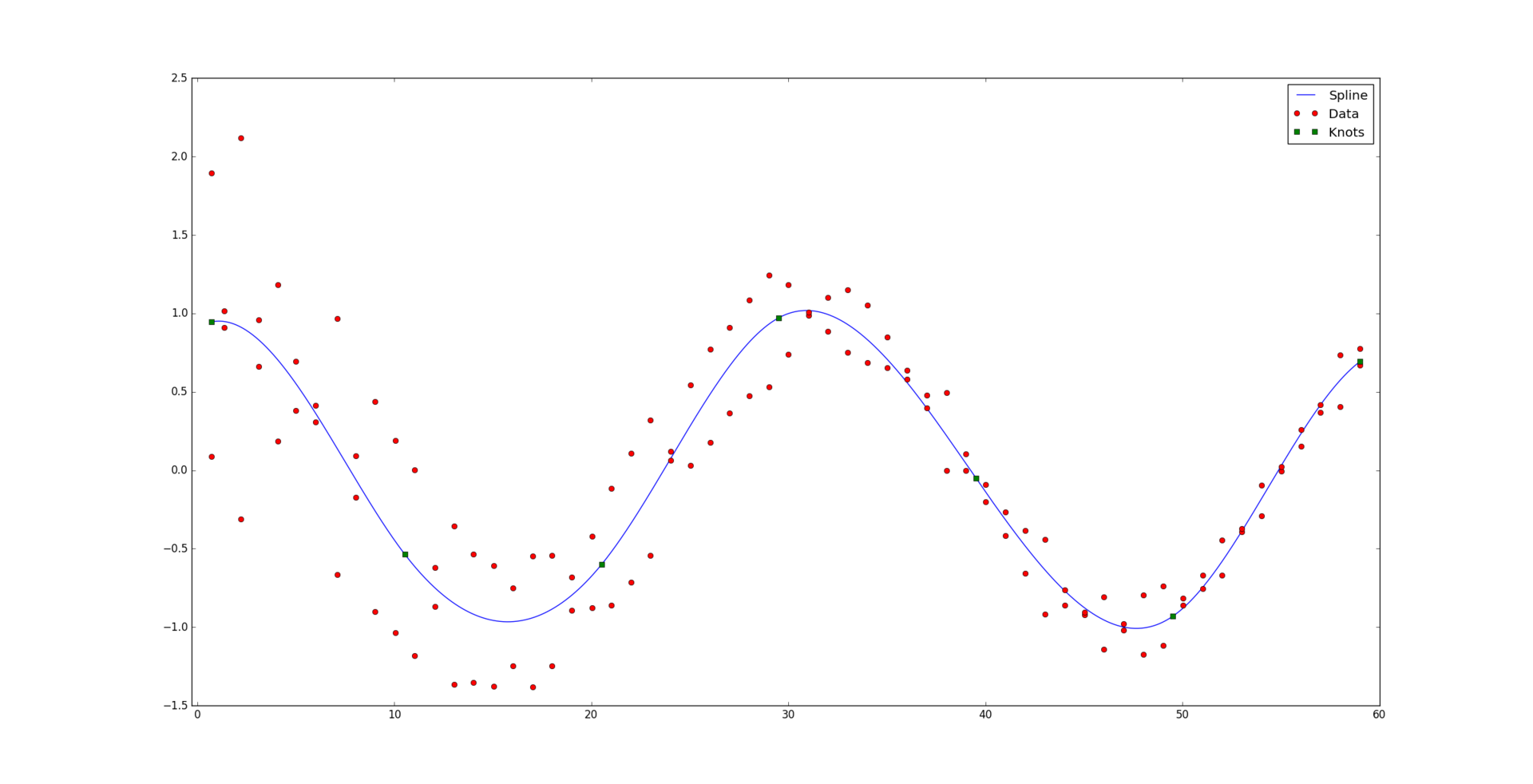
Под катом находится алгоритм, раскрывающий, каким образом сплайны позволяют строить подобную красивую регрессию: