Рубрика «случайность»

в 16:49, , рубрики: доверительный интервал, закон больших чисел, интуиция, математика, математическое ожидание, случайность, статистика, теория вероятностей, центральная предельная теорема

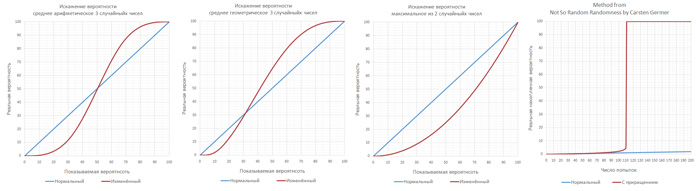
Недавно я написал статью про Закон Больших Чисел. Мы начали с такого вопроса

Бросим монетку тысячу раз и посчитаем, сколько выпало орлов. Странно ожидать, что выпадет ровно 500, но какое отклонение от этого числа типично?

Например, если зафиксировать конкретное отклонение, какова вероятность, что оно произойдёт? Если наоборот зафиксировать вероятность, то каким должно быть отклонение? И, наконец, если заданы и вероятность, и отклонение, то сколько раз надо бросать монетку, чтобы с заданной вероятностью попасть в эти рамки?

Читать полностью »

в 13:26, , рубрики: жребий, кнут, математика, математическое ожидание, монетка, случайность, сэмплирование, теория вероятностей, энтропия

Начнем наш сегодняшний путь с задачи

Три айтишника — Маша, Вася и Петя — пошли в поход. После ужина они решают, кто будет мыть посуду. Петя дежурит один, а Маша с Васей — вдвоём. Значит, нужно выбрать Петю с вероятностью 1⁄3, а Машу с Васей — с вероятностью Читать полностью »

в 16:46, , рубрики: Броуновское движение, графы, дисперсия, математика, монте-карло, случайность, теория вероятностей, электрические цепи

в 16:29, , рубрики: генератор случайных чисел, заблуждения, интуиция, искажение, математика, парадокс, случайность, теория вероятностей, философия науки
Что не так? Три парадокса теории вероятностей - 1

Парадокс двух детей Вы встретили на прогулке соседей с сыном. Известно, что у них двое детей. Какова вероятность, что второй — тоже мальчик?

Читать полностью »

в 17:55, , рубрики: алгоритм, дуализм, мультивселенная, рекурсия, симметрия, случайность, сознание
Фрактал Мандельброта

Фрактал Мандельброта

Что, если реальность — это алгоритм, который пишет сам себя?

Читать полностью »

в 11:00, , рубрики: задача о подсолнухе, математика, множества, Научно-популярное, порядок, случайность, хаос

Серьёзный прорыв в деле решения гипотезы 60-летней давности проливает свет на то, как при росте случайных систем в них начинает появляться порядок

Математики начинают укрощать «задачу о подсолнухе» - 1

Команда из математиков и специалистов по информатике, наконец, продемонстрировала прогресс в решении, на первый взгляд, простой задачи, терзавшей исследователей почти шесть десятилетий.

Эта задача, поставленная математиками Палом Эрдёшем и Ричардом Радо в 1960-м, касается того, как часто можно ожидать появления узоров, напоминающих подсолнух, в больших наборах объектах – например, в большом количестве точек, рассыпанном на плоскости. И хотя новый результат не решает гипотезу Эрдёша и Радо полностью, он продвигает понимание математиков в вопросе появления удивительно сложных структур в случайных скоплениях. Для этого в работе задачу переформулировали в терминах компьютерной функции, воспользовавшись преимуществами становящейся всё более тесной взаимосвязи между теоретической информатикой и чистой математикой.
Читать полностью »

в 8:30, , рубрики: Google, Pixel 3, информационная безопасность, обновление, ошибка, случайность, смартфоны
Google по ошибке позволила владельцам Pixel 3 уже сейчас получить обновление безопасности Android от 5 ноября 2019 года - 1

Скриншот меню обновления ОС Android владельца Pixel 3 от 31 октября 2019 года.

Одним из преимуществ для владельцев смартфонов Google Pixel является то, что эти устройства одни из первых получают самые новые обновления для ОС Android, в том числе закрывающие ошибки в системе безопасности. Следующее «гражданское» ежемесячное обновление безопасности для Android должно выйти 5 ноября 2019 года, но некоторые пользователи Google Pixel 3 и Pixel 3 XL, по данным портала «Android police», уже в конце октября случайно получили более раннюю версию этого обновления (Build QP1A.191105.003), предназначенную только для внутреннего тестирования среди специалистов и сотрудников Google. Такое происходит в Google уже не первый раз. Владельцы Pixel 3a, Pixel 3a XL прошлым летом в июне также получили тестовое июльское обновление безопасности на неделю раньше.
Читать полностью »

в 7:21, , рубрики: Gamedev, gamedevelopment, Дизайн игр, игровая механика, Игры и игровые приставки, манипулирование, манипуляция статистикой, разработка игр, расчеты, случайность, случайные числа, теория вероятности

Вычислять факт попадания в играх на основе полученной меткости можно по разному:
— сравнивая с одним псевдослучайным числом (которое тоже можно получать по разному [1]);
— сравнивая с наибольшим или наименьшим из двух псевдослучайных чисел;
— сравнивая среднее из двух и более случайных чисел (среднее тоже можно считать по разному).

Способы применения и искажения меткости в играх. Наглядные графики для сравнения - 1

Бонусы к меткости тоже можно реализовать по разному, вызывая тем самым у игроков раздражение по разными причинам.
Точно также по разному можно рассчитывать наносимый урон, особенно на основе дайсов (кубиков).
Все эти разные подходы влияют на игровой процесс: его сложность и предсказуемость. Каждый из них может оказаться удачным решением в зависимости от преследуемых целей, поэтому выгоднее всего делать выбор осознанно.
В статье будут представлены наглядные графики изменения реальных вероятностей в разных подходах, что позволит быстрее в них сориентироваться и принять лучшее решение.
Читать полностью »

в 5:01, , рубрики: Gamedev, gamedevelopment, RNG, seed, генератор псевдослучайных чисел, генератор случайных чисел, Дизайн игр, заблуждения, Игры и игровые приставки, манипуляции, разработка игр, случайность

Человеческий мозг по своей природе очень плохо умеет оценивать вероятность срабатывания случайных событий, на основании выданной числовой оценки. И довольно хорошо на основании качественных оценок. А все потому, что человек мысленно делает конвертацию числовых вероятностей в качественные оценки, и делает это очень субъективно:

  • 80% попадания выстрела в игре — ну это почти гарантированное попадание;
  • 80% того, что ваш товарищ хоть когда-нибудь отдаст долг — не-не-не, так не пойдёт, это слишком большой риск;
  • 5% получения критического урона он NPC врага — маловероятно, риск можно игнорировать;
  • 1% риск падения сосульки, если пройти под крышей с капающими метровыми сосульками — ещё чего, лучше обойти с другой стороны тротуара;
  • 51% вероятность выигрыша в мини-игре в большой РПГ — можно рассчитывать на то, что после 20 ставок я чуть-чуть выиграю или, как минимум, останусь при своих… через 20 ставок… как такое могло случиться, что я проиграл половину всего своего золота? Тут явно сломан генератор случайных чисел!

Заблуждения игроков при оценке рисков. Контроль генератора случайных чисел в разработке - 1

В статье будут рассмотрены следующие вопросы:

  • ошибочные допущения в оценке вероятностей;
  • конкретные примеры заблуждений игроков и фактические вероятности «редких» событий;
  • генератор случайных чисел (вообще-то псевдослучайных);
  • ранние простые генераторы псевдослучайных чисел на примере Final Fantasy I;
  • подходы к реализации случайных событий с воспроизводимостью и без;
  • примеры удачно внедренных разных подходов и манипуляции в Fire Emblem.

Читать полностью »

в 15:50, , рубрики: везение, Лайфхаки для гиков, случайность, удача

image

Считаете ли вы себя удачливым человеком? Были ли у вас в жизни неожиданности, сделавшие вашу жизнь лучше? Я не имею в виду крупные выигрыши в лотерею, но такие вещи, как внезапное получение рабочего места из-за болезни более сильного кандидата, или задержавшийся поезд, на который вы и сами опаздывали?

А, может, вы считаете себя неудачливым человеком? Пропустили собеседование из-за гриппа, или не попали на поезд из-за его отмены?

Или, возможно, вы не верите в удачу, и считаете, что удачу, или неудачу, человек делает сам, и успех в жизни зависит от тяжёлой работы и упорства. Конечно, даже вера в такой вариант жизни не объясняет её полностью – неважно, как упорно вы работали, отменённый поезд вам не вернуть. Всегда есть вещи, от вас не зависящие.
Читать полностью »

12
Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js