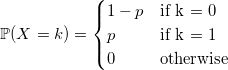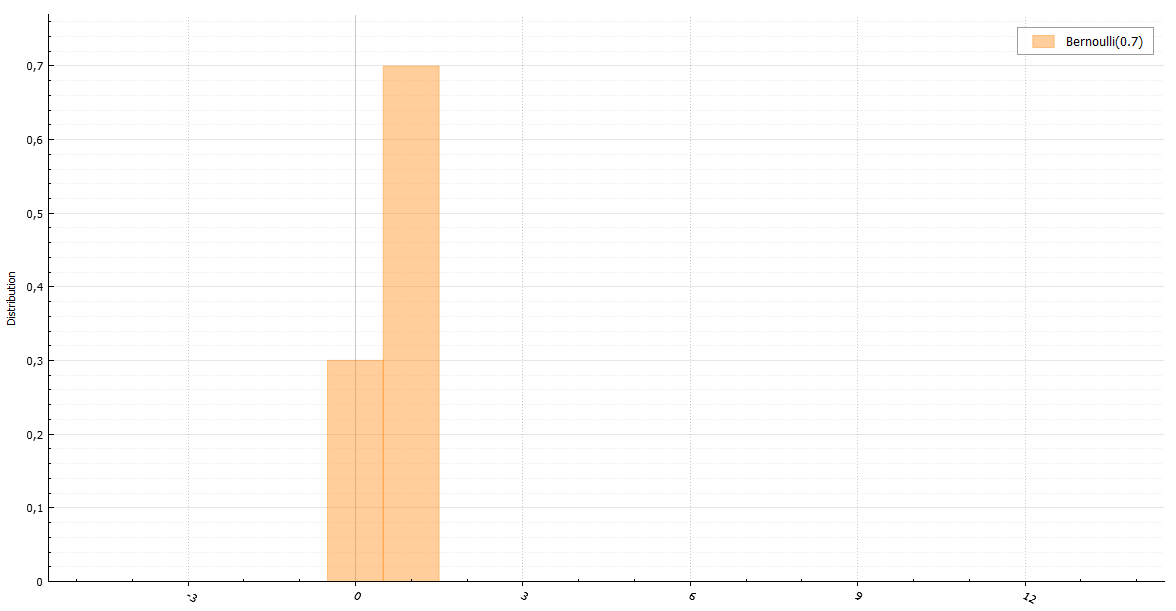Недавно меня попросили написать отзыв на автореферат кандидатской диссертации, в которой обсуждалось моделирование случайных величин с использованием Python и C++. Я разбираюсь в моделировании, но не в программировании. Обсуждая работу, я поинтересовался у соискателя, почему он выбрал эти инструменты и не рассматривал ли Excel. Он ответил, что в их среде Excel не используется. «А жаль», — подумал я. Особенно учитывая, что в работе выборки не превышали сотни элементов. Excel легко справляется даже с миллионом и имеет десятки встроенных функций для таких целей.
Рубрика «случайная величина»
Как в Excel сгенерировать случайную величину произвольного распределения
2025-02-11 в 7:01, admin, рубрики: Ланит, моделирование в Excel, непрерывные распределения, случайная величина, теория вероятностей, численные методыФильтр Калмана для минимизации энтропийного значения случайной погрешности с не Гауссовым распределением
2019-02-01 в 13:52, admin, рубрики: python, scipy, stats, Алгоритмы, законы распределения, математика, Научно-популярное, разработка под windows, Скалярный фильтр Калмана, случайная величина, фильтрация шумов
Введение
На Habr математическое описание работы фильтра Калмана и особенности его применения рассматривались в следующих публикациях [1÷10]. В публикации [2] в простой и доходчивой форме рассмотрен алгоритм работы фильтра Калмана (ФК) в модели «пространства состояний», Следует отметить, что исследование систем контроля и управления во временной области с помощью переменных состояния широко используется в последнее время благодаря простоте проведения анализа [11].
Публикация [8] представляет значительный интерес именно для обучения. Очень эффективен методический приём автора, который начал свою статью с рассмотрения распределения случайной погрешности Гаусса, рассмотрел алгоритм ФК и закончил простой итерационной формулой для подбора коэффициента усиления ФК. Автор ограничился рассмотрением распределения Гаусса мотивируя это тем, что при достаточно больших 
Теоретически такое утверждение, безусловно, справедливо, однако на практике число измерений в каждой точке диапазона не может быть очень большим. Сам R. E. Kalman получил результаты о минимуме ковариации фильтра на базе ортогональных проекций, без предположения о гауссовости ошибок измерений [12].
Целью настоящей публикации является исследование возможностей фильтра Калмана для минимизации энтропийного значения случайной погрешности с не Гауссовым распределением.
Для оценки эффективности фильтра Калмана при идентификации закона распределения или суперпозицией законов по экспериментальным данным воспользуемся информационная теорией измерений основанной на теории информации К. Шеннона, согласно которой информация, подобно физической величине, может быть измерена и оценена.
Читать полностью »
«Правда, чистая правда и статистика» или «15 распределений вероятности на все случаи жизни»
2016-09-30 в 7:46, admin, рубрики: f-критерий, f-распределение, f-тест, t-критерий, t-распределение, t-тест, z-критерий Фишера, z-распределение, z-тест, Алгоритмы, Анализ и проектирование систем, бета распределение, биноминальное распределение, гамма распределение, геометрическое рапределение, гипергеометрическое распределение, двойное показательное, двойное экспоненциальное, Занимательные задачки, критерий Пирсона, критерий согласия, критерий хи квадрат, математика, моделирование, нормальное распределение, отрицательное биноминальное, плотность вероятности, показательное распределение, профит фактор, распределение Бернулли, распределение Вейбулла, распределение Гаусса, распределение Коши, распределение Лапласса, распределение Паскаля, распределение Пирсона, распределение пуассона, распределение Стьюдента, распределение Фишера, распределение хи квадрат, распределение Эрланга, случайная величина, статистика, статистический тест, статитический анализ, теория вероятностей, тест Стьюдента, тест Фишера, экспоненциальное распределение Статистика приходит к нам на помощь при решении многих задач, например: когда нет возможности построить детерминированную модель, когда слишком много факторов или когда нам необходимо оценить правдоподобие построенной модели с учётом имеющихся данных. Отношение к статистике неоднозначное. Есть мнение, что существует три вида лжи: ложь, наглая ложь и статистика. С другой стороны, многие «пользователи» статистики слишком ей верят, не понимая до конца, как она работает: применяя, например, тест Стьюдента к любым данным без проверки их нормальности. Такая небрежность способна порождать серьёзные ошибки и превращать «поклонников» теста Стьюдента в ненавистников статистики. Попробуем поставить токи над i и разобраться, какие модели случайных величин должны использоваться для описания тех или иных явлений и какая между ними существует генетическая связь.
Статистика приходит к нам на помощь при решении многих задач, например: когда нет возможности построить детерминированную модель, когда слишком много факторов или когда нам необходимо оценить правдоподобие построенной модели с учётом имеющихся данных. Отношение к статистике неоднозначное. Есть мнение, что существует три вида лжи: ложь, наглая ложь и статистика. С другой стороны, многие «пользователи» статистики слишком ей верят, не понимая до конца, как она работает: применяя, например, тест Стьюдента к любым данным без проверки их нормальности. Такая небрежность способна порождать серьёзные ошибки и превращать «поклонников» теста Стьюдента в ненавистников статистики. Попробуем поставить токи над i и разобраться, какие модели случайных величин должны использоваться для описания тех или иных явлений и какая между ними существует генетическая связь.
Читать полностью »
Генераторы дискретно распределенных случайных величин
2016-01-15 в 22:54, admin, рубрики: Алгоритмы, генераторы случайных чисел, дискретное распределение, математика, Программирование, случайная величина, случайности не случайны, теория вероятностей, метки: генераторы случайных чисел, случайная величинаДанная статья является продолжением поста Генераторы непрерывно распределенных случайных величин. В этой главе учитывается, что все теоремы из предыдущей статьи уже доказаны и генераторы, указанные в ней, уже написаны. Как и ранее, у нас имеется некий базовый генератор натуральных чисел от 0 до RAND_MAX:
unsigned long long BasicRandGenerator() {
unsigned long long randomVariable;
// some magic here
...
return randomVariable;
}
С дискретными величинами все интуитивно понятнее. Функция распределения дискретной случайной величины:
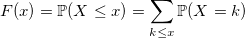
Несмотря на простоту распределений дискретных случайных величин, генерировать их подчас сложнее, нежели чем непрерывные. Начнем, как и в прошлый раз, с тривиального примера.
Распределение Бернулли