Мне очень нравится знаменитая цитата Ричарда Фейнмана:
«То, что я не могу создать, я не понимаю»
Рубрика «Регулярные выражения»
Радость создания хобби-программ
2025-06-30 в 13:01, admin, рубрики: Регулярные выражения, текстовый редактор, физический движок, хобби-проекты, шахматный движокРегулярные выражения простыми словами. Часть 3
2025-06-30 в 8:08, admin, рубрики: oarticle, regex, regexp, selctel, Регулярные выражения
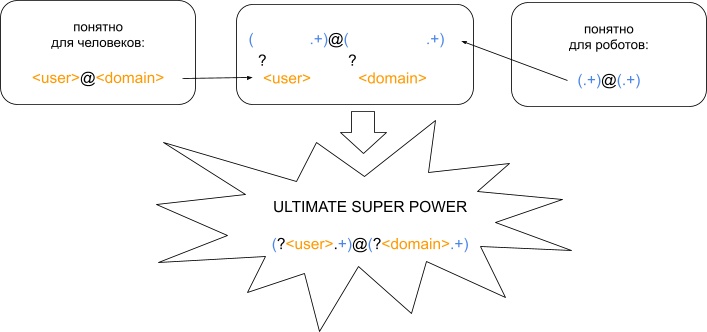
Разработчики делятся на три типа: тех, кто уже понимает регулярные выражения и порой решает сложные задачи одной строкой; тех, кто все еще боится их и всячески избегает; и тех, кто уже прочитал первую и вторую части этой серии статей и полон оптимизма разобраться с этими магическими письменами. Эта статья специально для третьих, чтобы обратно их напугать, ведь в этой части мы рассмотрим одну из самых сложных, но в буквальном смысле захватывающих тем.Читать полностью »
Самый быстрый способ нахождения гласной в строке
2025-06-23 в 13:01, admin, рубрики: cpython, работа со строками, Регулярные выражения, строки
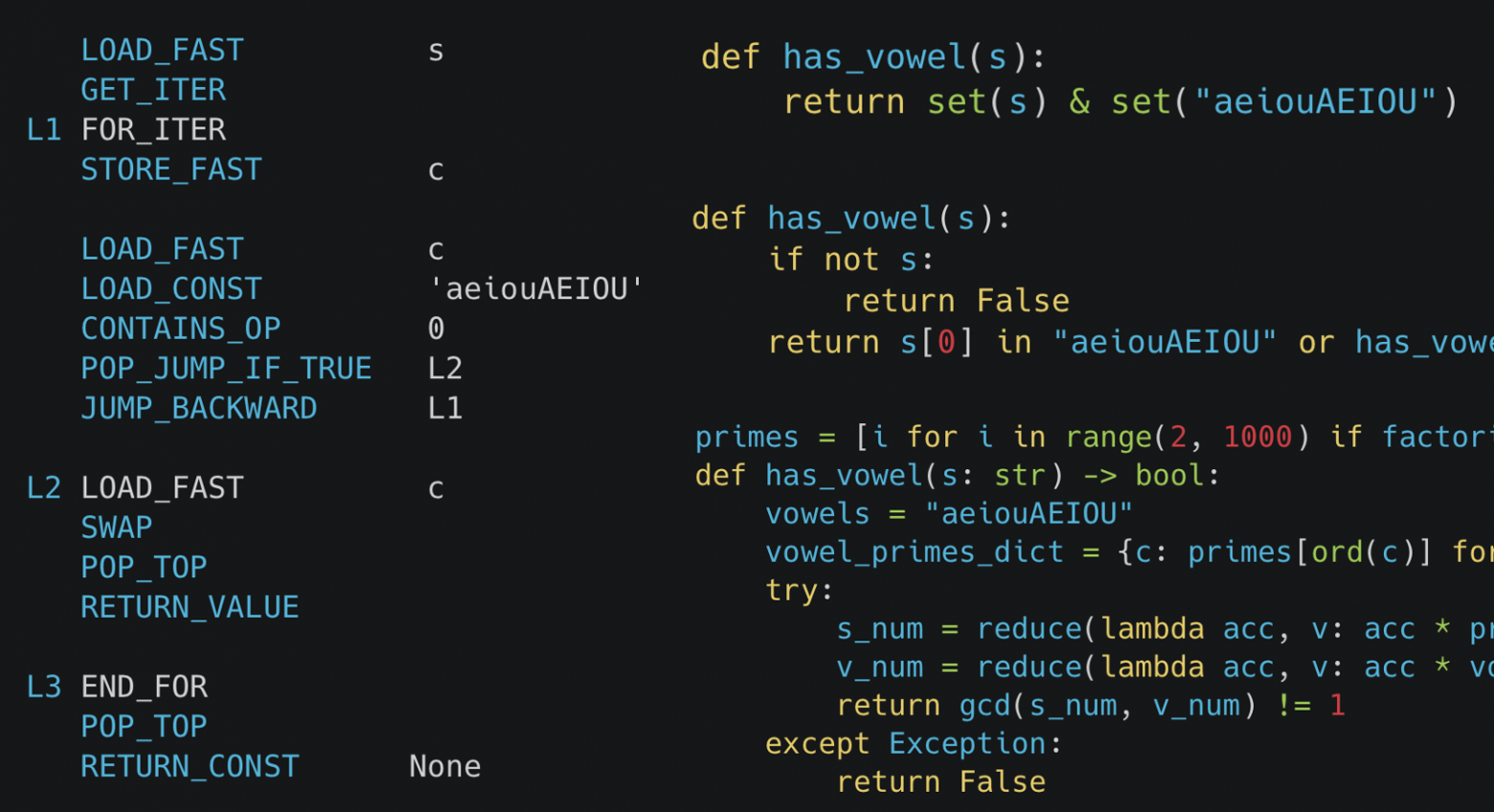
Недавно меня заинтересовала такая задача: как лучше всего определить, что в строке есть гласная?
Казалось бы, тривиальный вопрос, правда?
Регулярные выражения простыми словами. Часть 2
2024-12-04 в 8:39, admin, рубрики: oarticle, regexp, selectel, Регулярные выражения
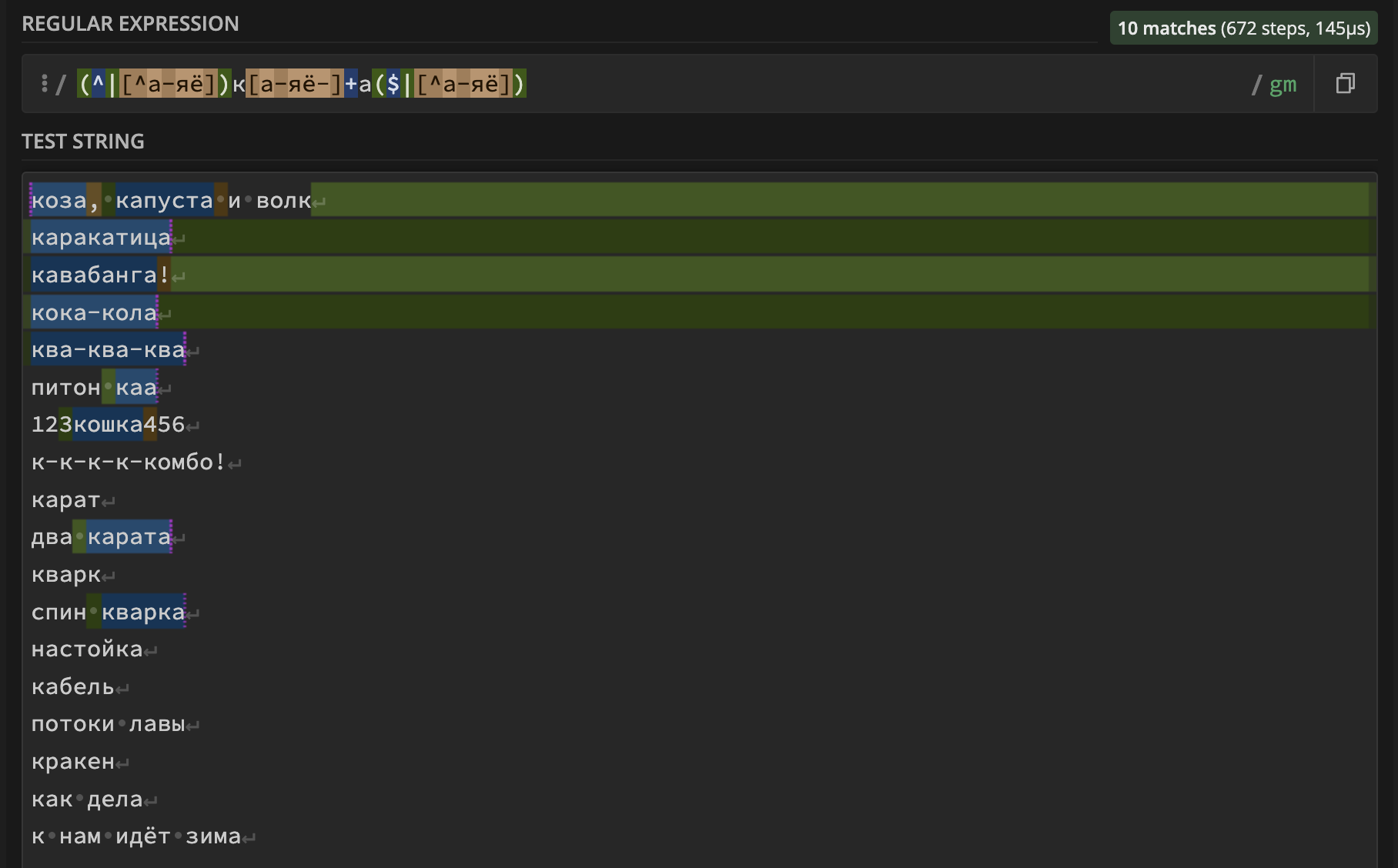
Разработчики делятся на три типа: те, кто уже понимает регулярные выражения и порой решает сложные задачи одной строкой; те, кто все еще боится их и всячески избегает; и те, кто уже прочитал первую часть этой серии статей и полон оптимизма разобраться с этими магическими письменами. Эта статья специально для третьих, чтобы им было проще стать первыми.Читать полностью »
Разбор регулярного выражения, проверяющего простоту чисел
2024-11-13 в 7:38, admin, рубрики: java, regex, regexp, простые числа, Регулярные выраженияВведение
Как-то я исследовал способы наиболее эффективного определения простоты числа и наткнулся на следующий код:
public static boolean isPrime(int n) {
return !new String(new char[n]).matches(".?|(..+?)\1+");
}Он меня заинтриговал. Хоть это, возможно, и не самый эффективный способ, но определённо один из наименее очевидных, поэтому мне стало любопытно. Каким образом соответствие регулярному выражению .?|(..+?)1+ должно показать, что число непростое (после его преобразования в унарную систему счисления)?
Регулярные выражения простыми словами. Часть 1
2024-10-07 в 12:00, admin, рубрики: oarticle, regex, regexp, selctel, Регулярные выражения
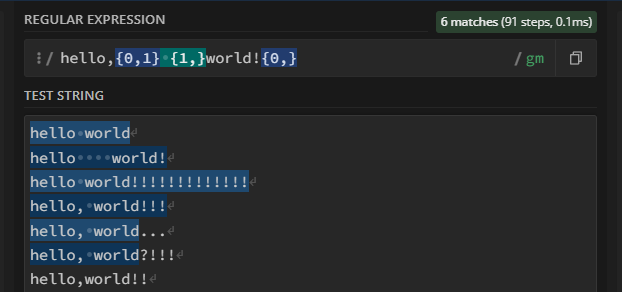
Разработчики делятся на два типа: тех, кто уже понимает регулярные выражения и порой решает сложные задачи одной строкой, и тех, кто все еще боится и всячески их избегает. Эта статья специально для вторых, чтобы им было проще стать первыми. Она либо поможет преодолеть «регекспофобию», либо усугубит ее. В любом случае, добро пожаловать под кат.Читать полностью »
find + mkdir полны по Тьюрингу
2024-08-20 в 10:55, admin, рубрики: find, fizzbuzz, GNU, mkdir, машина Тьюринга, полнота по Тьюрингу, Регулярные выражения
Введение
Мы покажем, что система, имеющая лишь команды GNU find и mkdir, полна по Тьюрингу.
Хорошо известно, что команды sed и awk сами по себе полны по Тьюрингу, но мне не удалось найти информации о Тьюринг-полноте find + mkdir.
Доказательство основано на реализации таг-системы.
Мы по порядку рассмотрим реализацию цикла, FizzBuzz и таг-системы.
Технические лайфхаки для конкурсов
2023-06-11 в 15:49, admin, рубрики: Excel, php, vba, visual basic for applications, Занимательные задачки, интернет-маркетинг, конкурсы, маркетинг, Регулярные выражения, социальные сети, Социальные сети и сообщества
Казалось бы, чего что сложного может быть в проведении конкурсов в социальных сетях. Но на практике всё не так просто, как кажется на первый взгляд.
Многие SMM-щики вынуждены проходить все круги ада, пока не автоматизируют максимум процессов при проведении нетипичных конкурсов. Поэтому хотим поделиться некоторыми из используемых нами технических лайфхаков.
Конкурс прогнозов
Если вы отказались от регулярных выражений, то теперь у вас три проблемы
2023-04-10 в 16:00, admin, рубрики: regex, regexp, ruvds_перевод, Блог компании RUVDS.com, композиция, ненормальное программирование, парсеры, парсинг данных, Программирование, Регулярные выражения
Известная шутка программистов гласит, что если решение вашей проблемы включает в себя парсинг текста при помощи регулярного выражения, то теперь у вас есть две проблемы. Некоторые программисты, прочитав шутку, решают попробовать иной подход. Возможно, регулярные выражения не так уж нужны. Возможно, задачу можно решить простым split строки или чем-то подобным. Однако другие могут задуматься немного глубже и задаться вопросом: «А если я сделаю нечто настолько дерзкое, что в результате получу три проблемы?» Мой пост написан в таком духе!
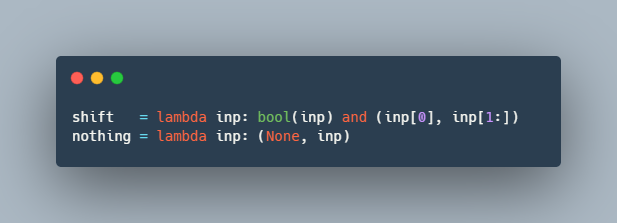
В нём используется код на Python, однако его легко можно адаптировать под любой язык с поддержкой функций высшего порядка.
Читать полностью »
Хватит использовать [a-zа-яё]: правильная работа с символами и категориями Unicode в регулярных выражениях
2023-01-27 в 12:15, admin, рубрики: regex, regexp, Программирование, Разработка веб-сайтов, регулярное выражение, Регулярные выражения, Совершенный код, типографикаUnicode – это набор символов, целью которого является определение всех символов и глифов всех человеческих языков, живых и мертвых. Поскольку всё больше и больше программ должны поддерживать несколько языков или просто любой язык, юникод в последние годы приобретает всё большую популярность. Использование различных наборов символов для разных языков может быть слишком обременительным для программистов и пользователей.
К сожалению, юникод привносит свои требования и подводные камни, когда речь заходит о регулярных выражениях.