Введение
По линейному программированию средствами Python мною в статье [1] было рассмотрено решение задачи оптимизации с функцией цели альтернативной к основной. Как было показано в статье приём с введением новых функций цели при рассмотрении одной общей задачи оптимизации значительно расширяет аналитические возможности метода. Поэтому логично выбрать и рассмотреть такой пример, в котором при решении общей задачи оптимизации можно сформулировать несколько альтернативных функций цели.
Постановка задачи
На примере задачи об оптимальной диете рассмотреть формирование различных альтернативных функций цели с необходимыми начальными условиями. Кроме этого разработать простой и единообразный интерфейс решения подобных задач с выводом результатов понятных конечному пользователю.
Формирование целевой функции и начальных условий для минимизации стоимости диеты
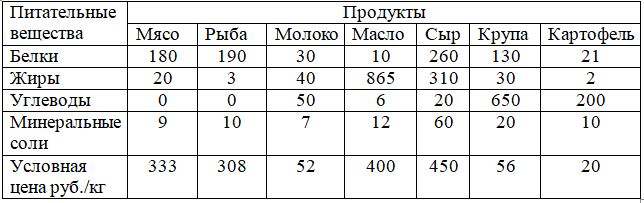
Для поддержания нормальной жизнедеятельности человеку необходимо потреблять в день не менее 118 г белков, 56 г жиров, 500 г углеводов и 28 г минеральных солей. Эти питательные вещества содержатся в разных количествах и разных пищевых продуктах.
В таблице приведено количество питательных веществ в различных продуктах в г/кг и условная цена этих продуктов за 1 кг. Необходимо составить дневной рацион, содержащий минимальную суточную норму питательных веществ при минимальной их стоимости.