Иногда для того, чтобы решить какую-то проблему, надо просто взглянуть на нее под другим углом. Даже если последние лет 10 подобные проблемы решали одним и тем же способом с разным эффектом, не факт, что этот способ единственный.
Есть такая тема, как отток клиентов. Штука неизбежная, потому что клиенты любой компании могут по множеству причин взять и перестать пользоваться ее продуктами или сервисами. Само собой, для компании отток — хоть и естественное, но не самое желаемое действие, поэтому все стараются этот отток минимизировать. А еще лучше — предсказывать вероятность оттока той или иной категории пользователей, или конкретного пользователя, и предлагать какие-то шаги по удержанию.
Анализировать и пытаться удержать клиента, если это возможно, нужно, как минимум, по следующим причинам:
- привлечение новых клиентов дороже процедур удержания. На привлечение новых клиентов, как правило, нужно потратить определенные деньги (реклама), в то время как существующих клиентов можно активизировать специальным предложением с особыми условиями;
- понимание причин ухода клиентов — ключ к улучшению продуктов и услуг.
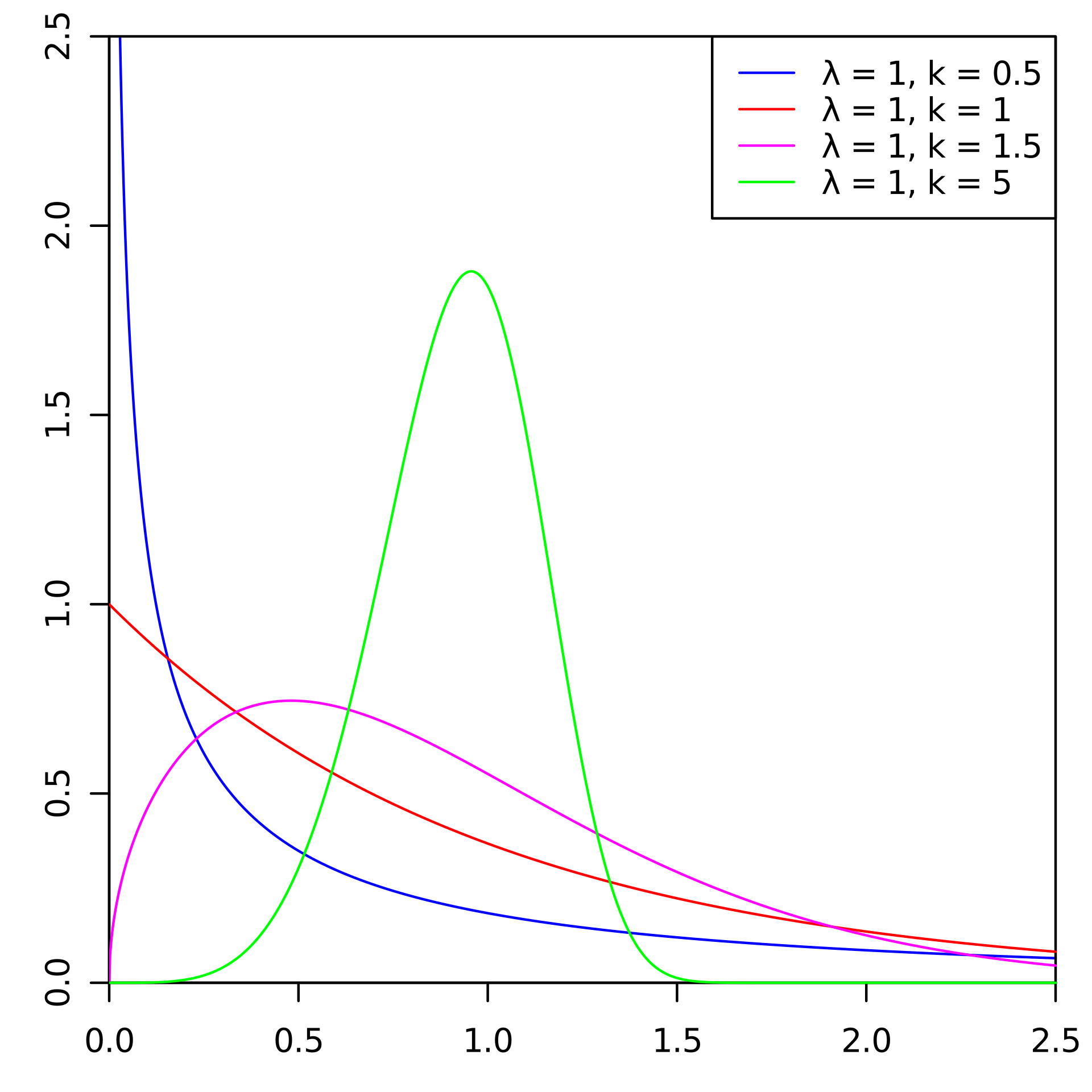
Существуют стандартные подходы к прогнозированию оттока. Но на одном из чемпионатов по ИИ мы решили взять и попробовать для этого распределение Вейбулла. Чаще всего его используют для анализа выживаемости, прогнозирования погоды, анализа стихийных бедствий, в промышленной инженерии и подобном. Распределение Вейбулла — специальная функция распределения, параметризуемая двумя параметрами 

В общем, вещь занятная, но для прогнозирования оттока, да и вообще в финтехе, использующаяся не так, чтобы часто. Под катом расскажем, как мы (Лаборатория интеллектуального анализа данных) это сделали, попутно завоевав золото на Чемпионате по искусственному интеллекту в номинации «AI в банках».
Читать полностью »