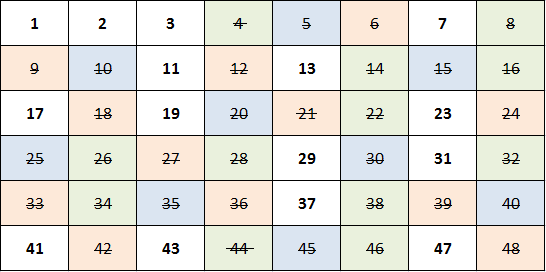
Код, графики, попытка анализа — все под катом.
Читать полностью »

Код, графики, попытка анализа — все под катом.
Читать полностью »
Всем привет! Это мой первый пост на Хабре, потому я представлюсь: меня зовут Костя, я разработчик C++, немного музыкант, начинающий ML инженер и любитель математики. Как не сложно догадаться этот пост будет о моём математическом хобби.
Простое число — это натуральное число, имеющее ровно два различных натуральных делителя — единицу и самого себя. Такие числа представляют огромный интерес. Дело в том, что никто так и не смог полностью понять и описать закономерность по которой простые числа располагаются в ряду натуральных чисел.
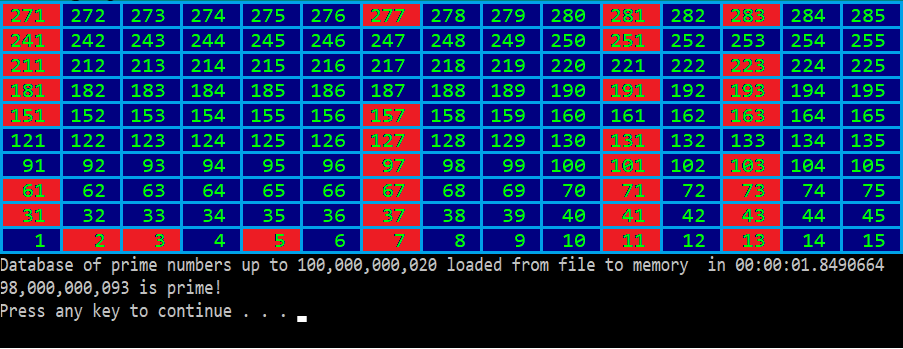
Самый известный алгоритм для нахождения всех простых чисел, не больших заданного, – решето Эратосфена. Он замечательно работает для чисел до миллиардов, может быть, до десятков миллиардов, если аккуратно написан. Однако каждый, кто любит развлекаться с простыми числами, знает, что их всегда хочется иметь под рукой как можно больше. Как-то раз мне для решения одной задачи на хакерранке понадобилась in-memory база данных простых чисел до ста миллиардов. При максимальной оптимизации по памяти, если в решете Эратосфена представлять нечетные числа битовым массивом, его размер будет около 6 гигабайт, что в память моего ноутбука не влезало. Существует модификация алгоритма, гораздо менее требовательная по памяти (делящая исходный диапазон чисел на несколько кусков и обрабатывающая по одному куску за раз) – сегментированное решето Эратосфена, но она сложнее в реализации, и результат целиком в память все равно не влезет. Ниже предлагаю вашему вниманию алгоритм почти такой же простой, как и решето Эратосфена, но дающий двукратную оптимизацию по памяти (то есть, база данных простых чисел до ста миллиардов будет занимать около 3 гигабайт, что уже должно влезать в память стандартного ноутбука).
Читать полностью »
Представьте, что вас окружает бесконечно высокая стена, а о том, что находится за стеной абсолютно ничего неизвестно. Теперь представьте, что олицетворением данной стены является вот это уравнение:
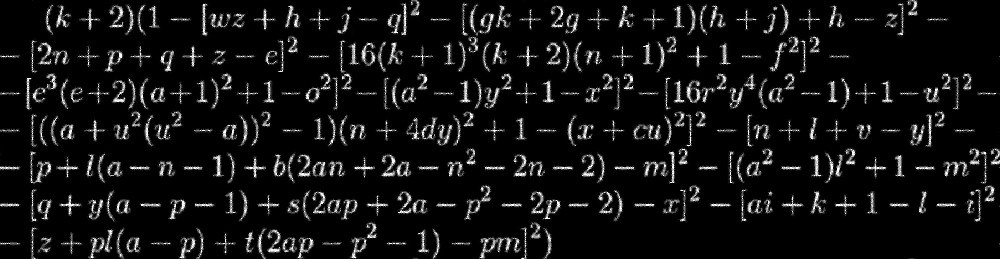
Эту метафору будет проще понять, если провести аналогию с черной дырой: мы не знаем, что находится под ее горизонтом событий, и чтобы это узнать нам нужно придумать способ, как туда добраться. Нечто подобное существует в мире математики. Данное уравнение — это настоящая «формула» простого числа, но чтобы ею пользоваться, нам нужно придумать, как искать подходящие {a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, w, v, x, y, z}.
Черная дыра и данное уравнение — это предельные состояния чего-то реального и абстрактного. И, если о первом существует достаточно догадок и представлений, то о втором, практически ничего не известно. Но, что если это действительно «математическая» черная дыра. Разве вам не интересно что может произойти, если мы попадем
Читать полностью »

Значимость простых чисел, как в повседневном применении, так и во всех отраслях математики, невозможно переоценить. Мы спокойно полагаемся на их особые свойства, используя их как фундамент бесчисленного количества элементов нашего общества, ведь они являются неделимой частью самой ткани природы. Простые числа, устойчивые к любому делению на множители, часто называют «атомами» мира математики. Карл Саган сказал о них так:
Очень важен статус простых чисел как фундаментальных строительных блоков всех чисел, которые сами являются строительными блоками нашего понимания Вселенной.
В природе и в нашей жизни простые числа используются повсюду: цикады выстраивают по ним свои жизненные циклы, часовщики применяют их для вычисления тиканья, а в авиационных двигателях с их помощью балансируется частота воздушных импульсов. Однако все эти области применения бледнеют на фоне факта, знакомого каждому криптографу: простые числа находятся в самом сердце современной компьютерной безопасности, то есть они напрямую несут ответственность за защиту всего. Видите замок в адресной строке браузера? Да, это значит, что используется двухключевое «рукопожатие», основанное на простых числах. Как защищается при покупках ваша кредитная карта? Тоже при помощи криптографии на основе простых чисел.
Однако несмотря на то, что мы постоянно полагаемся на их уникальные свойства, простые числа оставались для нас неуловимыми. На протяжении всей истории математики величайшие умы пытались доказать теорему о предсказании чисел, являющихся простыми, или о том, как далеко друг от друга они должны располагаться.Читать полностью »
 «Самое большое простое число 232582657-1. И я с гордостью утверждаю, что запомнил все его цифры… в двоичной форме».
«Самое большое простое число 232582657-1. И я с гордостью утверждаю, что запомнил все его цифры… в двоичной форме».
Карл Померанс
Число называется простым, если оно имеет только два различных делителя: единицу и само себя. Задача поиска простых чисел не дает покоя математикам уже очень давно. Долгое время прямого практического применения эта проблема не имела, но все изменилось с появлением криптографии с открытым ключом. В этой заметке рассматривается несколько способов поиска простых чисел, как представляющих исключительно академический интерес, так и применяемых сегодня в криптографии.
Читать полностью »
В предыдущих сериях мы взглянули на дробные числа с несколько необычных ракурсов. В этой серии, после введения и некоторой теоретической базы, попробуем собрать всё в удобном виде и получить пользу от имеющейся информации.
Читать полностью »
Решето Сундарама в сети представлено большим количеством источников краткой справочной информации. Тем не менее, я решил изложить то, что хотел бы прочитать сам в начале изучения теоретико-числовых алгоритмов.
Решето Сундарама входит в тройку известнейших методов генерации простых чисел. Сейчас к нему принято относиться как к некоторой экзотике по причине плохой вычислительной сложности: O(N(logN)). Однако асимптотика – асимптотикой, а на практике в 32-битном диапазоне просеивания Аткин, например, перегоняет Сундарама только при тщательной оптимизации.
Реализации решета Аткина, имеющие хождение в интернете, не превосходят решето Сундарама ни по временным характеристикам, ни по эффективности использования памяти. Так что метод Сундарама вполне можно использовать как вспомогательный инструмент при экспериментах с более продвинутыми алгоритмами.
Читать полностью »
Посвящается памяти Джона Форбса Нэша-младшего
Вы ведь помните, что такое «простые числа»? Эти числа не делятся ни на какие другие, кроме самих себя и 1. А теперь я задам вопрос, которому уже 3000 лет:
Придумайте суждение или формулу, которые (хотя бы с грехом пополам) прогнозируют, каким будет следующее простое число, (в любом заданном ряду чисел), и ваше имя навечно будет связано с одним из величайших достижений человеческого мозга. Вы встанете в один ряд с Ньютоном, Эйнштейном и Гёделем. Разберитесь в поведении простых чисел, и можете потом всю жизнь почивать на лаврах.
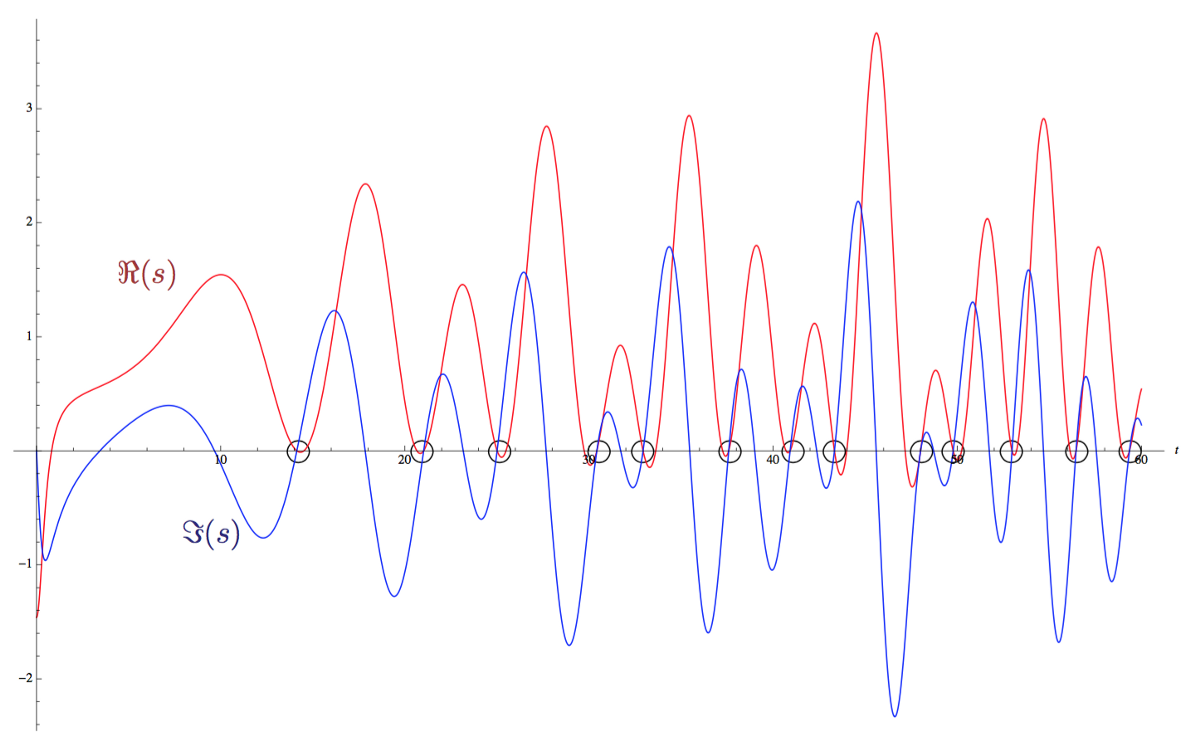
Свойства простых чисел изучались многими великими людьми в истории математики. С первого доказательства бесконечности простых чисел Евклида до формулы произведения Эйлера, связавшей простые числа с дзета-функцией. От формулировки теоремы о простых числах Гаусса и Лежандра до её доказательства, придуманного Адамаром и Валле-Пуссеном. Тем не менее, Бернхард Риман до сих пор считается математиком, сделавшим единственное крупнейшее открытие в теории простых чисел. В его опубликованной в 1859 году статье, состоявшей всего из восьми страниц, были сделаны новые, ранее неизвестные открытия о распределении простых чисел. Эта статья по сей день считается одной из самых важных в теории чисел.
После публикации статья Римана оставалась главным трудом в теории простых чисел и на самом деле стала основной причиной доказательства в 1896 году теоремы о распределении простых чисел. С тех пор было найдено несколько новых доказательств, в том числе элементарные доказательства Сельберга и Эрдёша. Однако до сих пор остаётся загадкой гипотеза Римана о корнях дзета-функции.
Читать полностью »