Зачастую при разработке алгоритмов мы упираемся в предел вычислительной сложности, который, казалось бы, преодолеть невозможно. Преобразование Фурье имеет сложность 




Читать полностью »
Рубрика «преобразование фурье» - 2
Преобразование Фурье. The Fast and the Furious
2018-12-28 в 13:58, admin, рубрики: Алгоритмы, звук, математика, преобразование фурье, цифровая обработка сигналовАмплитудная модуляция на пальцах
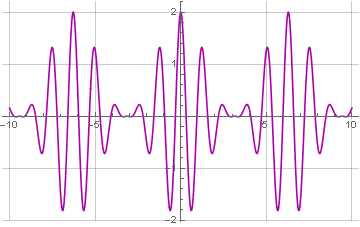
2018-07-04 в 19:21, admin, рубрики: wolfram mathematica, амплитудная модуляция, математика, преобразование фурьеВ недавней статье «Амплитудная модуляция произвольного сигнала» её автор довольно сумбурно попытался представить своё понимание формирования спектра при амплитудной модуляции. Но отсутствие иллюстраций и избыток математики с привлечением интегральных преобразований помешало сообществу понять мысли автора и оценить статью по достоинству; в то время как тема это достаточно простая — и рассмотреть которую мы попробуем ещё раз, на этот раз с картинками и привлечением Wolfram Mathematica.
Итак, идея амплитудной модуляции состоит в том, чтобы передавать низкочастотный сигнал — голос или музыку — модулируя высокочастотный (несущий) сигнал, многократно превышающий слышимый диапазон и занимающий узкую полосу частот в радиоэфире. Сама модуляция осуществляется простым умножением сигнала на несущий:
Невероятно эффектная цветомузыка на Arduino и светодиодах
2017-12-11 в 14:58, admin, рубрики: arduino, diy или сделай сам, ардуинщик, вечеринка, звук, красиво, легко, начинающим, Новый Год, преобразование фурье, сделай сам, спектрограмма, цветомузыкаС наступающим!
Приближается Новый год, а значит, пора срочно создавать настроение! Ну и как всегда в это время года рождаются десятки электронных схем различных цветомузыкальных установок.
Чего только самобытные мастера не придумают. От трехцветных моргалок до лазерных многолучевых установок с управлением по MIDI интерфейсу.

Как большой поклонник, так называемых адресных светодиодов, хочу показать вам самую простою, но удивительную цветомузыку. Я вообще такой ни разу не видел. Пока не собрал за один вечер. Итак, визуализатор звука!
Читать полностью »
О классификации методов преобразования Фурье на примерах их программной реализации средствами Python
2017-09-25 в 16:03, admin, рубрики: python, математика, преобразование фурье, разработка под windows, решение дифференциальных уравненийВведение
Публикации по методу Фурье условно можно разделить на две группы. Первая группа так называемых познавательных публикаций, например, [1,2].
Вторая группа публикаций касается применения преобразований Фурье в технике, например, при спектральном анализе [3,4].
Ни в коем случае не умоляя достоинства этих групп публикации стоит признать, что без классификации, или хотя бы попытки осуществить такую классификацию, получить системное представление о методе Фурье, по моему мнению, затруднительно.
Задачи публикации
Провести классификацию методов преобразования Фурье на примерах их программной реализации средствами Python. При этом для облегчения чтения использовать формулы только в программном коде с соответствующими пояснениями.
Гармонический анализ и синтез
Гармоническим анализом называют разложение функции f(t), заданной на отрезке [0, Т] в ряд Фурье или в вычислении коэффициентов Фурье по формулам.
Гармоническим синтезом называют получение колебаний сложной формы путем суммирования их гармонических составляющих (гармоник).
#!/usr/bin/python
# -*- coding: utf-8 -*
from scipy.integrate import quad # модуль для интегрирования
import matplotlib.pyplot as plt # модуль для графиков
import numpy as np # модуль для операций со списками и массивами
T=np.pi; w=2*np.pi/T# период и круговая частота
def func(t):# анализируемая функция
if t<np.pi:
p=np.cos(t)
else:
p=-np.cos(t)
return p
def func_1(t,k,w):# функция для расчёта коэффициента a[k]
if t<np.pi:
z=np.cos(t)*np.cos(w*k*t)
else:
z=-np.cos(t)*np.cos(w*k*t)
return z
def func_2(t,k,w):#функция для расчёта коэффициента b[k]
if t<np.pi:
y=np.cos(t)*np.sin(w*k*t)
else:
y=-np.cos(t)*np.sin(w*k*t)
return y
a=[];b=[];c=4;g=[];m=np.arange(0,c,1);q=np.arange(0,2*np.pi,0.01)# подготовка списков для численного анализа
a=[round(2*quad(func_1, 0, T, args=(k,w))[0]/T,3) for k in m]# интеграл для a[k], k -номер гармоники
b=[round(2*quad(func_2, 0, T, args=(k,w))[0]/T,3) for k in m]# интеграл для b[k], k -номер гармоники
F1=[a[1]*np.cos(w*1*t)+b[1]*np.sin(w*1*t) for t in q]#функции для гармоник
F2=[a[2]*np.cos(w*2*t)+b[2]*np.sin(w*2*t) for t in q]
F3=[a[3]*np.cos(w*3*t)+b[3]*np.sin(w*3*t) for t in q]
plt.figure()
plt.title("Классический гармонический анализ функции n при t<pi f(t)=cos(t) при t>=pi f(t)=-cos(t)")
plt.plot(q, F1, label='1 гармоника')
plt.plot(q, F2 , label='2 гармоника')
plt.plot(q, F3, label='3 гармоника')
plt.xlabel("Время t")
plt.ylabel("Амплитуда А")
plt.legend(loc='best')
plt.grid(True)
F=np.array(a[0]/2)+np.array([0*t for t in q-1])# подготовка массива для анализа с a[0]/2
for k in np.arange(1,c,1):
F=F+np.array([a[k]*np.cos(w*k*t)+b[k]*np.sin(w*k*t) for t in q])# вычисление членов ряда Фурье
plt.figure()
P=[func(t) for t in q]
plt.title("Классический гармонический синтез")
plt.plot(q, P, label='f(t)')
plt.plot(q, F, label='F(t)')
plt.xlabel("Время t")
plt.ylabel("f(t),F(t)")
plt.legend(loc='best')
plt.grid(True)
plt.show()
Применение преобразования Фурье для создания гитарного тюнера на Android. Часть 1
2017-07-17 в 11:58, admin, рубрики: java, Алгоритмы, бпф, гармоника, дпф, звуковая волна, преобразование фурье, разработка мобильных приложений, тюнер для гитары, частота дискретизации
В основе спектрального анализа звуковых данных лежит алгоритм, который носит название преобразование Фурье. При раскладывании исходного звукового сигнала на частотные составляющие, отдельные частоты называются гармониками. Основная гармоника определяет высоту звучания, а второстепенные гармоники определяют его тембр. Есть достаточно много мобильных приложений, которые используют преобразование Фурье для того, чтобы отобразить весь спектр частот (гармоник). Так же, есть мобильные приложения, которые служат для настройки гитар. Они работают по принципу: основная гармоника находится по самому высокому значению амплитуды в спектре. Такое утверждение не совсем верно, потому что основная гармоника определяется самой наименьшей из всех кратных этой гармонике, либо шагом между гармониками. Возникает необходимость найти способ, который позволит отобразить значение основной гармоники в спектре звукового сигнала.
В первой части статьи мы рассмотрим принцип работы дискретного преобразование Фурье, а также возможность записывать звуковые данные с Android устройства с помощью класса AudioRecord. Читать полностью »
Практическое применение преобразования Фурье для обработки сигналов
2017-03-16 в 15:30, admin, рубрики: бпф, математика, обработка сигналов, преобразование фурье, Программирование, программирование микроконтроллеров, реальное времяВведение
Книги и публикации по цифровой обработке сигналов пишут авторы зачастую не догадывающиеся и не понимающие задач стоящих перед разработчиками. Особенно это касается систем, работающих в реальном времени. Эти авторы отводят себе скромную роль бога, существующего вне времени и пространства, что вызывает некоторое недоумение у читателей подобной литературы. Данная публикация имеет целью развеять недоумения, возникающие у большинства разработчиков, и помочь им преодолеть «порог вхождения», для этих целей в тексте сознательно используется аналогии и терминология сферы программирования.
Данный опус не претендует на полноту и связность изложения.
Читать полностью »
Функции шума и генерирование карт
2017-02-17 в 6:45, admin, рубрики: fft, Алгоритмы, генерация ландшафта, преобразование фурье, разработка игр, функции шума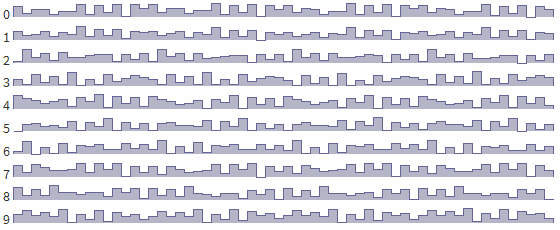
Когда я изучал обработку аудиосигналов, мой мозг проводить аналогии с процедурным генерированием карт. В статье излагаются принципы, связывающие обработку сигналов с генерированием карт. Не думаю, что открыл что-то новое, но некоторые выводы были для меня в новинку, поэтому я решил записать их и поделиться с читателями. Я рассматриваю только простые темы (частоту, амплитуду, цвета шума, использование шума) и не затрагиваю другие темы (дискретные и непрерывные функции, фильтры FIR/IIR, быстрое преобразование Фурье, комплексные числа). Математика статьи в основном связана с синусоидами.
Эта статья посвящена концепциям, начиная с самых простейших и заканчивая более сложными. Если вы хотите перейти сразу к генерированию рельефа с помощью функций шума, то изучите другую мою статью.
Читать полностью »
Ошибка процессора Intel Skylake приводит к зависанию компьютера во время сложных вычислений
2016-01-12 в 12:21, admin, рубрики: Broadwell, Haswell, intel, Prime95, Skylake, Блог компании Positive Technologies, вычисления, ит-инфраструктура, преобразование фурье, ПроцессорыГруппа немецких ученых из немецкого сообщества hardwaluxx.de обнаружила ошибку в работе процессоров Intel Skylake, приводящую к зависанию компьютера в процессе осуществления сложных вычислений. Позднее математики из проекта добровольных вычислений по поиску простых чисел Мерсенна (GIMPS) подтвердили наличие проблемы. Баг проявился в ходе работ по поиску простых чисел Мерсенна с помощью инструмента Prime95. Читать полностью »
Ограниченность преобразования Фурье или почему стоит доверять своему слуху
2015-12-28 в 9:59, admin, рубрики: fft, Алгоритмы, преобразование фурье, принцип неопределённости, Работа со звуком, распознавание музыкиПоследние несколько десятков лет задача распознавания аккордов музыкальной композиции ставилась довольно часто. Казалось бы, этот не столь оригинальный сервис был и остается довольно распространенным среди приложений, работающих со звуком (Ableton, Guitar Pro), однако универсального, срабатывающего всегда алгоритма не существует до сих пор. В этой статье я постараюсь раскрыть одну из множества причин неидеальной работы подобных сервисов на примере алгоритмов, использующих в своей основе преобразование Фурье.
Большинство аудиоформатов хранит информацию в виде зависимости амплитуды от времени (например, .wav) или в виде коэффициентов частотного преобразования (.mp3, .aac, .ogg), однако современные сложные алгоритмы цифровой обработки сигналов работают с частотной составляющей звуков. Приходится иметь дело с двойным переходом, из амплитудной области в частотную, затем обратно. На данный момент осуществление такого переход без потерь в качестве является достаточно распространенной проблемой с множеством неоднозначных решений.
Читать полностью »
Стимпанк-компьютер Альберта Майкельсона
2014-12-01 в 18:01, admin, рубрики: История ИТ, преобразование фурье, старое железоОказывается, ещё в 19 веке существовали вычислительные машины, способные осуществлять сложнейшие математические расчёты. Один из уникальных экземпляров — гармонический анализатор Альберта Майкельсона. Прибор выполнял преобразование Фурье. Эта функция сегодня широко используется в информатике, обработке сигналов, физике, теории чисел, комбинаторике, теории вероятностей, криптографии и других областях.
В честь 100-летия гармонического анализатора Майкельсона опубликована бесплатная электронная книга с великолепными иллюстрациями, где описывается принцип действия этого замечательного прибора.