Цель этой статьи не в том, чтобы дать строгое математическое определение преобразованию Фурье - это бесчисленное количество раз уже сделано другими авторами, а на примерах показать его "механический" смысл и пояснить почему оно работает.
Читателю понадобятся знания математики и физики на уровне 9 класса средней школы. Я предполагаю, что вы знаете теорему Пифагора, чему равен синус и косинус угла в прямоугольном треугольнике и что такое синусоида.
В конце статьи мы применим полученные знания для решения стандартной задачи декодирования телефонных номеров, сохранённых в аудиофайл в виде Читать полностью »
Уравнение пьезопроводности, которое также известно как уравнение диффузии или уравнение теплопроводности - это наиболее распространенное дифференциальное уравнение, которое, наряду с волновым уравнением, возникает во многих приложениях мат-физики при моделировании процессов протекающих в жидкостях и передачи тепла.
В одной из предыдущих статей я рассказал о математических алгоритмах, позволяющих проверить простоту очень большого числа. Но в основе всех тех алгоритмов лежит одна базовая операция — перемножение двух больших чисел. Именно операции длинного умножения занимают 99,9% времени выполнения любого теста простоты. Как же умножение реализуется на практике? Говорят, что при помощи Читать полностью »
Всем привет!
В цифровой обработке сигналов оконные функции широко используются для ограничения сигнала во времени и их названия хорошо известны всем, кто так или иначе сталкивался с дискретным преобразованием Фурье: Ханна, Хэмминга, Блэкмана, Харриса и прочие. Но являются ли они достаточными, можно ли придумать что-то новое и есть ли в этом смысл?
В этой статье мы рассмотрим вывод оконной функции с новыми свойствами, используя Wolfram Mathematica. Предполагается также, что читатель имеет общие представления о цифровой обработке сигналов в контексте обсуждаемого вопроса и как минимум знаком со статьёй из википедии.
Пять лет назад на Хабре была опубликована статья «Печать и воспроизведение звука на бумаге» — о системе создания и проигрывания спектрограмм. Затем, полтора года назад Meklon опубликовал квест, в котором такая чёрно-белая логарифмическая спектрограмма стала одним из этапов. По авторскому замыслу, её надо было распечатать на принтере, отсканировать смартфоном с приложением-проигрывателем, и воспользоваться таким образом «надиктованным» паролем.
У меня в тот момент не было в досягаемости ни принтера, ни смартфона, так что меня заинтересовали два аспекта задачи:
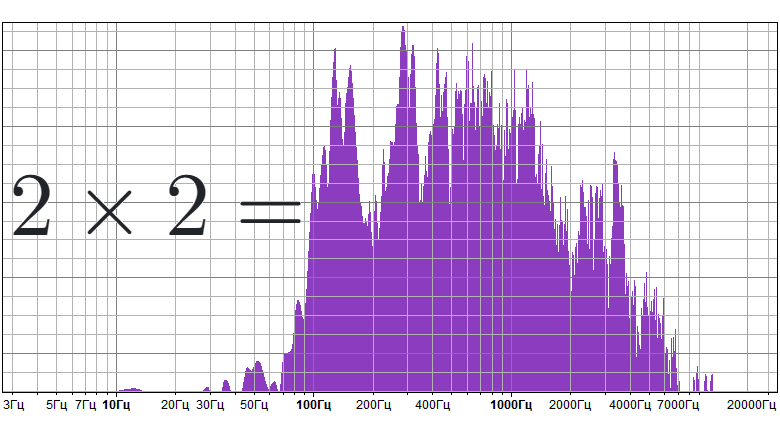
Скорее всего, вам известны следующие соотношения еще со школы:
Когда вы в детстве впервые познакомились с этой формулой, скорее всего, вашим первым чувством была боль из-за того, что эту формулу надо запомнить. Это очень плохо, потому что на самом деле вам не нужно запоминать эту формулу — она сама выводится, когда вы поворачиваете треугольник на бумаге. На самом деле, я делаю то же самое, когда записываю эту формулу. Это толкование будет очевидным к середине этой статьи. Но сейчас, чтобы оставить все веселье на потом и отодвинуть момент, когда вы скажете "Эврика!", давайте подумаем, а зачем нам вообще задумываться об этой формуле.
Зачастую при разработке алгоритмов мы упираемся в предел вычислительной сложности, который, казалось бы, преодолеть невозможно. Преобразование Фурье имеет сложность 
, а быстрый вариант, предложенный около 1805 года Гаусом1 (и переизобретенный в 1965 году Джеймсом Кули и Джоном Тьюки) 
. В данной статье хочу вам показать, что можно получить результаты преобразования за линейное время 
или даже достичь константной сложности 
при определенных условиях, которые встречаются в реальных задачах.
Читать полностью »
