Главная

Рубрика «погрешности округления»

Исправляем графический баг Mass Effect, возникающий на современных процессорах AMD

2020-07-27 в 6:19, admin, рубрики: amd, AMD FX, AMD Ryzen, intel, Игры и игровые приставки, обратная разработка, отладка, погрешности округления, Процессоры, реверс-инжиниринг, точность представления чисел

Введение

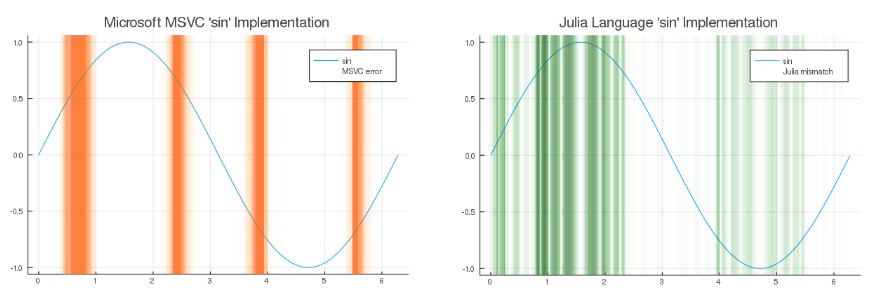
Mass Effect — популярная франшиза научно-популярных RPG. Первая часть сначала была выпущена BioWare в конце 2007 года эксклюзивно для Xbox 360 в рамках соглашения с Microsoft. Спустя несколько месяцев, в середине 2008 года, игра получила порт на PC, разработанный Demiurge Studios. Порт был достойным и не имел заметных недостатков, пока в 2011 году AMD не выпустила свои новые процессоры на архитектуре Bulldozer. При запуске игры на PC с современными процессорами AMD в двух локациях игры (Новерия и Илос) возникают серьёзные графические артефакты:

Исправляем графический баг Mass Effect, возникающий на современных процессорах AMD - 2

Да, выглядит некрасиво.

Хоть это и не делает игру неиграбельной, такие артефакты раздражают. К счастью, решение существует, например, можно отключить освещение консольными командами или модифицировать карты игры, удалив поломанные источники освещения, но, похоже, никто никогда так и не понял полностью причины этой проблемы. В некоторых источниках утверждается, что эту проблему позволяет устранить и мод FPS Counter, но мне не удалось найти информацию о нём: исходный код мода, похоже, не выложен онлайн, а документация о том, как мод исправляет ошибку, отсутствует.

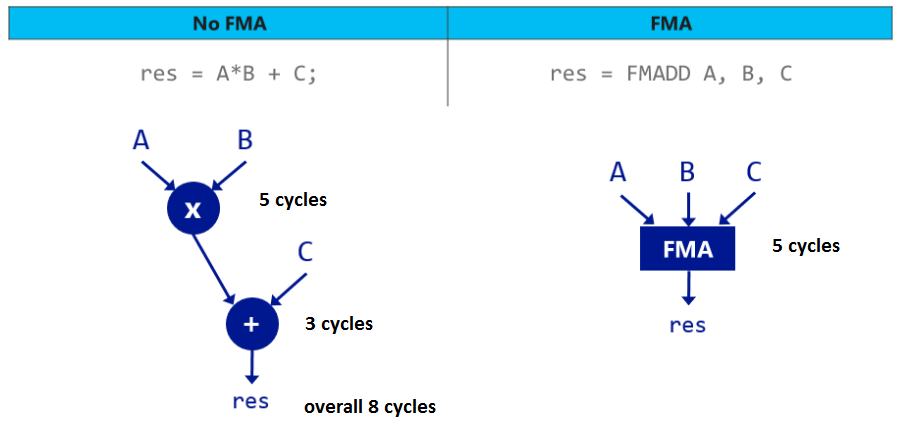
Почему эта проблема так интересна? Баги, возникающие только на оборудовании отдельных производителей, встречаются довольно часто, и в играх они встречаются уже много десятилетий. Однако, по моей информации, это единственный случай, когда проблема с графикой вызвана процессором, а не графической картой. В большинстве случаев проблемы возникают у продуктов определённого производителя GPU и никак не касаются CPU, однако в данном случае всё совсем наоборот. Поэтому эта ошибка уникальна, а значит, её стоит исследовать.
Читать полностью »

Алгоритм Кэхэна: как получить точную разность произведений

2019-11-14 в 7:51, admin, рубрики: double, float, fma, simd, Алгоритмы, двойная точность, математика, погрешности округления, числа с плавающей запятой

Недавно я вернулся к анализу погрешностей чисел с плавающей запятой, чтобы усовершенствовать некоторые детали в следующей редакции книги Physically Based Rendering. Числа с плавающей запятой — интересная область вычислений, полная сюрпризов (хороших и плохих), а также хитрых трюков, позволяющих избавиться от неприятных неожиданностей.

В процессе работы я наткнулся на этот пост на StackOverflow, из которого узнал об изящном алгоритме точного вычисления $a times b-c times d$ .

Но прежде чем приступать к алгоритму, нужно понять, что же такого хитрого в выражении $a times b-c times d$ ? Возьмём $a=33962.035$ , $b=-30438.8$ , $c=41563.4$ и $d=-24871.969$ . (Это реальные значения, которые получились у меня во время запуска pbrt.) При 32-битных значениях float получаем: $a times b=-1.03376365 times 10^9$ и $c times d=-1.03376352 times 10^9$ . Выполняем вычитание, и получаем $-128$ . Но если выполнить вычисления с двойной точностью, а в конце преобразовать их во float, то получится $-75.1656$ . Что произошло?

Проблема в том, что значение каждого произведения может сильно выйти за нижнюю границу $-1 times 10^9$ , где расстояние между представимыми значениями с плавающей запятой очень велико — 64. То есть при округлении $a times b$ и $c times d$ по отдельности до ближайшего представимого float, они превращаются в числа, кратные 64. В свою очередь, их разность будет кратной 64, и не останется никакой надежды, что она станет к $-75.1656$ ближе, чем $-64$ . В нашем случае результат оказался ещё дальше из-за того, как два произведения были округлены в $-1 times 10^9$ . Мы напрямую столкнёмся со старым добрым катастрофическим сокращением¹.
Читать полностью »