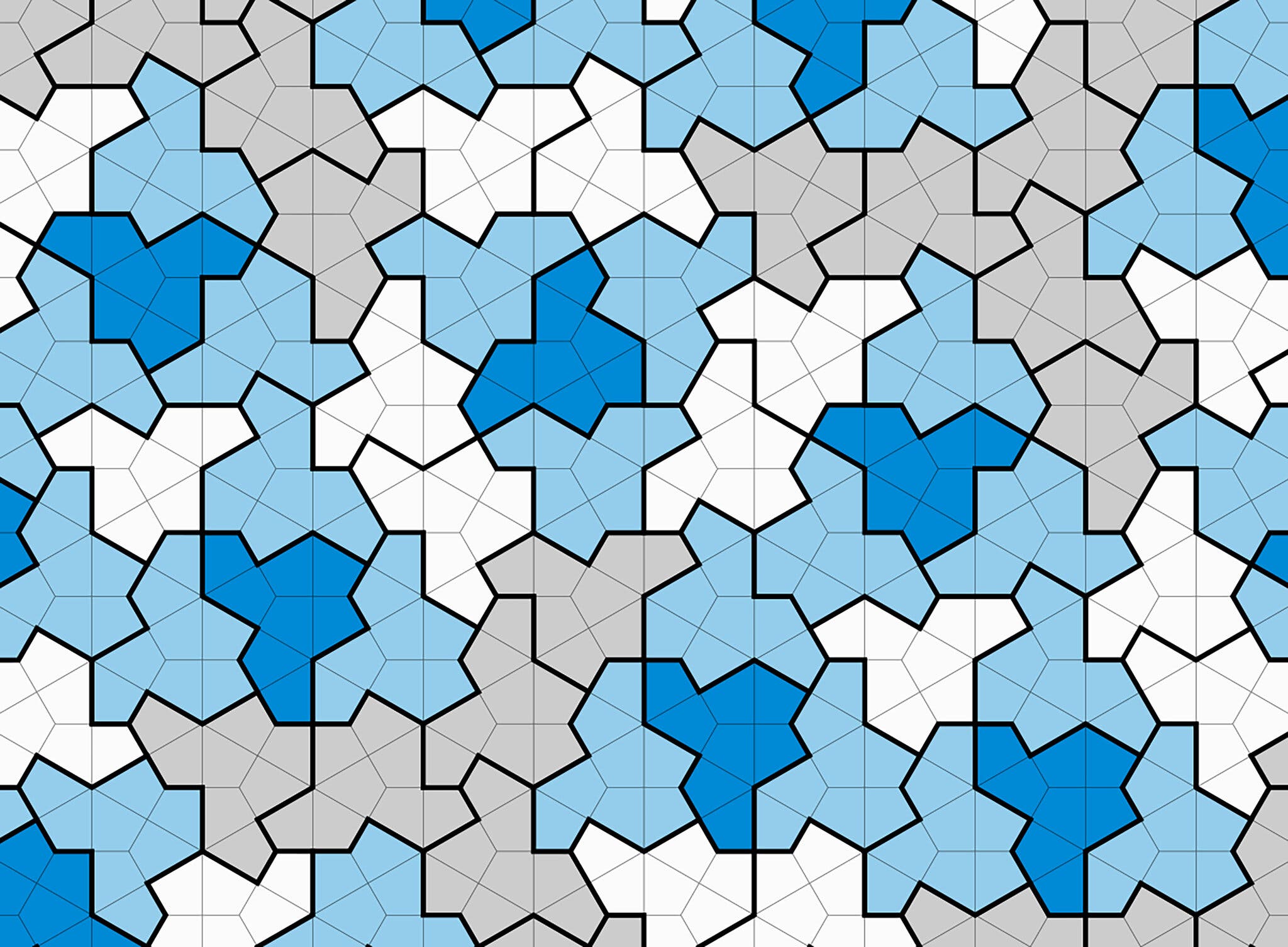
В ноябре прошлого года, после десяти лет неудачных попыток, Дэвид Смит, самопровозглашенный «любитель фигур» из Бридлингтона в Восточном Йоркшире, Англия, заподозрил, что, возможно, он наконец-то решил давнюю задачку в математике замощения плоскости: иначе говоря, он решил, что нашёл «эйнштейна».
В менее поэтичных терминах, «эйнштейн» — это «апериодическая моноплитка», фигура, которая покрывает плоскость или бесконечную двумерную плоскую поверхность неповторяющимся образом. (Термин «эйнштейн» происходит от немецкого «ein stein» или «один камень», в более свободной трактовке — «одна плитка» или «одна фигура»). Ваши обычные обои или кафельный пол представляют собою часть бесконечного узора, который периодически повторяется; при смещении или «переносе» узор может быть точно наложен сам на себя. Апериодическая плитка не обладает такой «трансляционной симметрией», и математики давно ищут единственную фигуру, которая могла бы покрыть плоскость такой плиткой. Эта задача известна под названием «проблемы Эйнштейна».
Читать полностью »

