Рубрика «плавающая запятая»

в 13:01, , рубрики: floating point, fpu, ieee 754, ruvds_статьи, плавающая запятая, плавающая точка, погрешности округления, числа с плавающей запятой

Ни одна реализация элементарных функций не соответствует стандарту IEEE 754 - 1


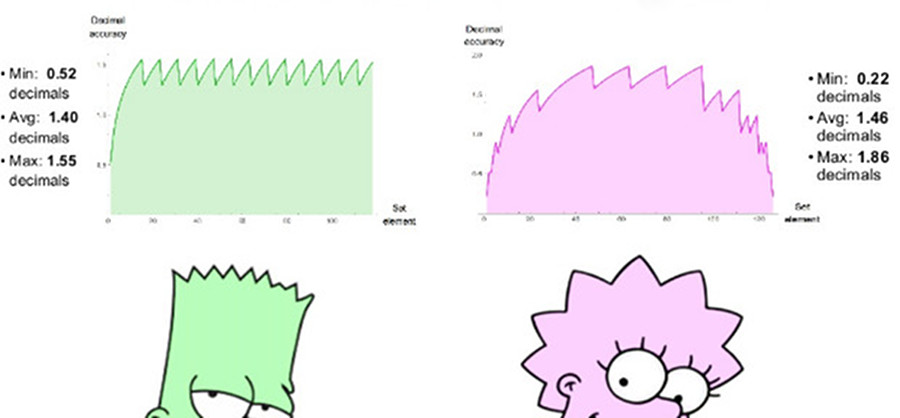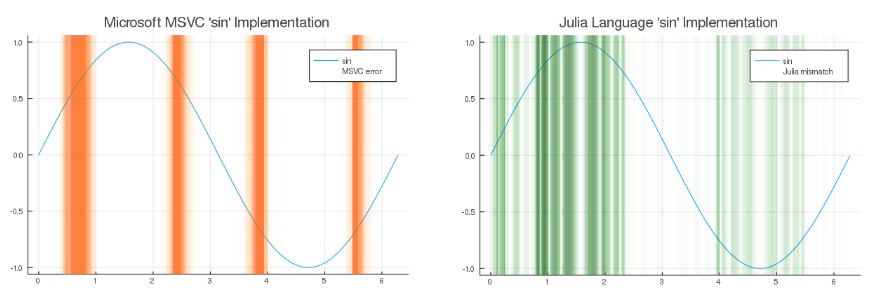
Введённый в 1985 году стандарт IEEE-754 для чисел с плавающей запятой был предназначен для решения проблемы разнородности реализаций чисел с плавающей запятой, мешавших портируемости кода, а также для повышения стабильности между платформами.

Он получил широкое применение и многократно пересматривался в течение прошедших лет. Если вы когда-нибудь работали с любыми вещественными числами в своих приложениях, то они, вероятно, отвечали этому стандарту.

Моя работа в течение последнего года заключалась в анализе погрешности различных математических функций, накопления этой погрешности и способов её уменьшения при помощи различных программных паттернов. Одной из исследованных мной тем были базовые математические функции, используемые в функциях активации нейронных сетей, а также способы их аппроксимации для повышения производительности. В процессе работы нам пришлось столкнуться с противодействием со стороны людей, активно стремящихся к корректной реализации математических функций и к соответствию их стандартам, в частности, к соблюдению обеспечения корректности одной наименее значимой единицы измерения (unit in last place, ULP) для элементарных функций.

Я был заинтересован в дальнейшей работе по аппроксимации этих функций, поэтому приступил к исследованию того, каким образом они гарантируют корректность, и если они корректны только на 1 ULP, то где располагаются ошибки в области определения функции.

В процессе изучения я обнаружил, что ни одна из популярных математических библиотек, используемых во множестве сфер вычислений, на самом деле не выполняет корректное округление в соответствии с требованиями любой версии IEEE 754 после первой редакции 1985 года.Читать полностью »

в 11:33, , рубрики: BF16, floating point, fp16, fp32, FP64, fp8, плавающая запятая, формат с плавающей запятой, числа с плавающей запятой
FP32, FP16, BF16 и FP8 — разбираемся в основных типах чисел с плавающей запятой - 1

Привет! Сегодня давайте поговорим о том, как современные вычисления на GPU стали более гибкими и эффективными благодаря различным форматам чисел с плавающей запятой (FP64, FP32, FP16, BFLOAT16 и FP8Читать полностью »

в 13:58, , рубрики: floating point, floatingpoint, fp16, fp32, fpu, ieee 754, INT8, квантизация, плавающая запятая, Тензорные ядра

Привет! С вами снова ServerFlow, и сегодня мы решили погрузиться в увлекательный мир чисел с плавающей запятой. Вы когда-нибудь задумывались, почему существуют разные виды этих чисел и как они влияют на производительность наших процессоров и видеокарт? Как малые числа с плавающей запятой помогают развивать нейросети и искусственный интеллект? Давайте вместе разберемся в этих вопросах, раскроем тайны стандарта IEEE 754 и узнаем, какое значение имеют большие и маленькие числа с плавающей запятой в современных вычислениях.

Стандарт IEEE 754

Читать полностью »

в 10:58, , рубрики: decimal, DPD, float, floating point, компьютер, математика, плавающая запятая, плавающая точка, технологии

*Все примеры здесь рассматриваются для 64 битных чисел(все примеры аналогичны и для других значений), если не указано иное.

Читать полностью »

в 7:14, , рубрики: плавающая запятая

в 5:31, , рубрики: double, floating point, java, абсолютное значение, математика, модуль, плавающая запятая, Программирование

Кажется, задача вычисления абсолютного значения (или модуля) числа совершенно тривиальна. Если число отрицательно, давайте сменим знак. Иначе оставим как есть. На Java это будет выглядеть примерно так:

public static double abs(double value) {
  if (value < 0) {
    return -value;
  }
  return value;
}

Вроде бы это слишком просто даже для вопроса на собеседовании на позицию джуна. Есть ли тут подводные камни?

Читать полностью »

в 15:01, , рубрики: CUDA, opencl, Wolfram, wolfram language, wolfram mathematica, абсолютная точность, Алгоритмы, ассоциативные массивы, Блог компании Wolfram Research, векторизация, вычисления, дебаг, компиляция, компиляция в c, машинная точность, мемоизация, оптимизация кода, отладка, плавающая запятая, правила замены, Программирование, распараллеливание, символьные вычисления, списки, точность, ускорение кода, функциональное программирование, хеш-таблицы, хэширование, шаблоны

Скачать файл с кодом и данные можно в оригинале поста в моем блоге

Картинка к вебинару и посту взята не просто так: в определенном смысле символьное ядро Wolfram Language можно сравнить с Таносом — если бы его мощь была бы направлена в правильное русло, он мог бы стать самым мощным и полезным «добряком». Так же и с символьным ядром Wolfram — его чудовищную мощь нужно правильно использовать, а если это делать не так, оно может стать настоящим «злом», замедляющим все очень сильно. Начинающие разработчики не знают многих важнейших парадигм, идей и принципов языка Wolfram Language, пишут код, который на самом деле дико неэффективен и после этого разочаровываются, хотя тут нет вины Wolfram Language. Эту ситуацию призвана исправить эта статья.

Мне довелось работать с Wolfram Language начиная с (уже довольно далекого) 2005 года (тогда еще была версия Mathematica 5.2, сейчас уже 12-я). За эти почти 15 лет произошло очень много: добавились тысячи новых встроенных функций и областей, в которых они работают (машинное обучение, точная геометрия, работа с аудио, работа в вебе, облачные возможности, глубокая поддержка единиц измерения, интеграция с базами данных Wolfram|Alpha, географические вычисления, поддержка работы с CUDA, Python, распараллеливание операций и многое многое другое), появились новые сервисы — облако Wolfram Cloud, широко известная система вычислительных значeний Wolfram|Alpha, репозиторий функций, репозиторий нейросетей и пр.
Читать полностью »

в 15:47, , рубрики: c++, float, posit, quire, высокая производительность, плавающая запятая, плавающая точка, Программирование, суперкомпьютеры, числа с плавающей запятой

Месяц Posit объявлен на Хабре открытым, а значит я не могу пройти мимо и проигнорировать обрушившуюся на них критику. В предыдущих сериях:

Новый подход может помочь нам избавиться от вычислений с плавающей запятой
Posit-арифметика: победа над floating point на его собственном поле. Часть 1
Posit-арифметика: победа над floating point на его собственном поле. Часть 2
Испытания Posit по-взрослому

Думаю многие из вас могут с ходу вспомнить хотя бы один случай из истории, когда революционные идеи на момент своего становления наталкивались на неприятие сообществом экспертов. Как правило, виной такому поведению выступает обширный багаж уже накопленных знаний, не позволяющий взглянуть на старую проблему в новом свете. Таким образом, новая идея проигрывает по характеристикам устоявшимся подходам, ведь оценивается она только теми метриками, которые считались важными на предыдущем этапе развития.

Именно с таким неприятием на сегодняшний день сталкивается формат Posit: критикующие зачастую просто “не туда смотрят“ и даже банально неправильно используют Posit в своих экспериментах. В данной статье я попытаюсь объяснить почему.Читать полностью »

в 3:05, , рубрики: floating point, open source, posit, Анализ и проектирование систем, математика, ненормальное программирование, плавающая запятая, плавающая точка, Программирование

Часть 1

4. Количественное сравнение числовых систем

4.1. Определение десятичной точности

Posit-арифметика: победа над floating point на его собственном поле. Часть 2 - 1

Точность обратна ошибке. Если у нас есть пара чисел x и y (ненулевых и одного знака), расстояние между ними в порядках величин составляет $mid log_{10}( x / y )mid$ десятичных порядков, это та же самая мера, которая определяет динамический диапазон между самым маленьким и самым большим представимым положительным числом x и y. Идеальным распределением десяти чисел между 1 и 10 в вещественной системе счисления было бы не равномерное распределение чисел по порядку от 1 до 10, а экспоненциальное: $1, 10^{1/10}, 10^{2/10},..., 10^{9/10}, 10$. Это шкала децибел, долгое время используемая инженерами для выражения отношений, например, 10 децибел — это десятикратное отношение. 30db означает коэффициент $10^3=1000$. Отношение 1db — это коэффициент около 1,26, если вы знаете значение с точностью 1db, вы имеете точность 1 десятичный знак. Если вы знаете величину с точностью 0,1 db, Это означает 2 знака точности, и т.п. Формула десятичной точности — $log_{10}(1/mid log_{10}(x/y)mid)=-log_{10}(mid log_{10}(x/y)mid )$, где x и y — либо корректные значения, вычисленные с использованием систем округления, таких, какие используются в форматах float и posit, либо верхние и нижние границы, если используются строгие системы, использующие интервалы, или значения valid.
Читать полностью »

в 3:05, , рубрики: floating point, open source, posit, Анализ и проектирование систем, математика, ненормальное программирование, плавающая запятая, плавающая точка, Программирование

Часть 2

От переводчика: Тема формата Posit уже была на хабре здесь, но без существенных технических подробностей. В этой публикации я предлагаю вашему вниманию перевод статьи Джона Густафсона (автора Posit) и Айзека Йонемото, посвящённой формату Posit.
Так как статья имеет большой объём, я разделил её на две части. Список ссылок находится в конце второй части.

Posit-арифметика: победа над floating point на его собственном поле. Часть 1 - 1

Новый тип данных, называемый posit, разработан в качестве прямой замены чисел с плавающей точкой стандарта IEEE Standard 754. В отличие от ранней формы — арифметики универсальных чисел (unum), стандарт posit не требует использования интервальной арифметики или операндов переменного размера, и, как и float, числа posit округляются, если результат не может быть представлен точно. Они имеют неоспоримые преимущества над форматом float, включая больший динамический диапазон, большую точность, побитовое совпадение результатов вычислений на разных системах, более простое аппаратное обеспечение и более простую поддержку исключений. Числа posit не переполняются ни в сторону бесконечности, ни до нуля, и «нечисла» (Not aNumber, NaN) — это действия, а не битовые комбинации. Блок обработки posit имеет меньшую сложность, чем FPU стандарта IEEE. Он потребляет меньшую мощность, и занимает меньшую площадь кремния, таким образом, чип может выполнять существенно больше операций над числами posit в секунду, чем FLOPS, при тех же аппаратных ресурсах. GPU и процессоры глубокого обучения, в частности, могут выполнять больше операций на ватт потребляемой мощности, что позволит повысить качество их работы.
Читать полностью »

12
Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js