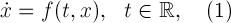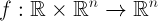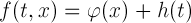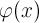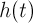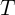
Этот топик продолжает серию моих статей на Хабре, посвященных исследованию аттрактора Лоренца.
Часть 1. Критический взгляд на аттрактор Лоренца
Часть 2. Динамическая система Лоренца и вычислительный эксперимент
Часть 3. О существовании периодических решений в системе Лоренца
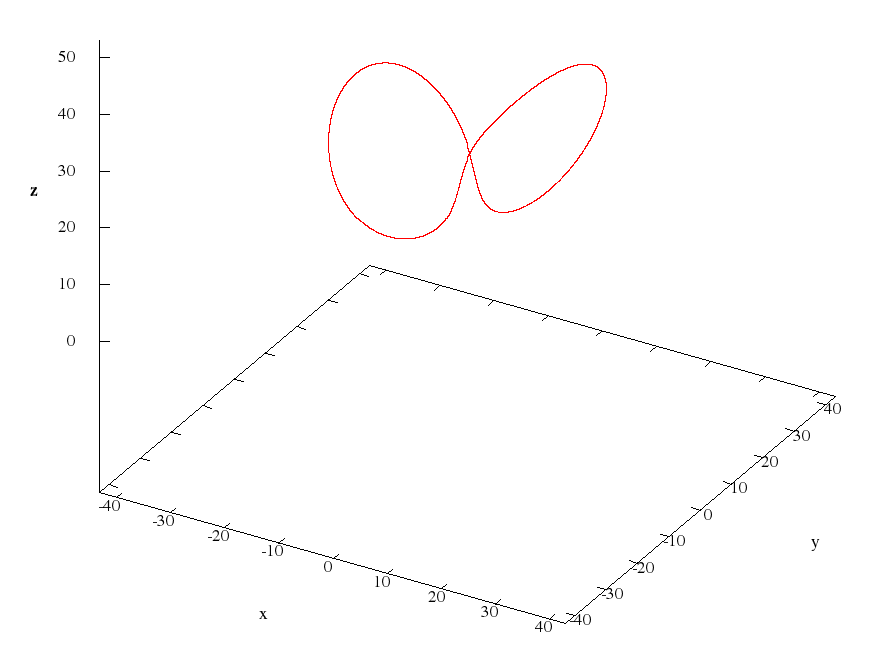
Часть 4. Три цикла в аттракторе Лоренца
Итак, рассмотрим нелинейную систему дифференциальных уравнений, введенную Эдвардом Лоренцом в 1963 году:
где
классические значения параметров системы.Читать полностью »
Изучая иностранную литературу, на днях наткнулся на работы [1, 2] профессора Мичиганского университета Дивакара Вишваната (Divakar Viswanath) об итерационном алгоритме вычисления периодических орбит динамических систем, основанном на методе Линдштедта-Пуанкаре (ЛП) (для ознакомления с ним рекомендую книгу [3, с. 408-411]). Преимуществом данного метода является то, что он не требует численного интегрирования дифференциального уравнения, поэтому может быть применён к построению и неустойчивых циклов. Читать полностью »
Это третий мой топик на Хабре (часть 1 и часть 2), посвященный динамической системе Лоренца. Я продолжаю заниматься исследованием вопроса о существовании периодических решений (циклов) в этой системе. Удалось получить интересный результат при определенном соотношении ее параметров.
Читать полностью »
В прикладной математике иногда возникает задача построения периодических решений нормальной системы обыкновенных дифференциальных уравнений вида
где функция 
представляет собой сумму
многомерного многочлена 
и тригонометрического полинома 
, являющегося 
-периодической векторной функцией.
Многие из теорем существования периодических решений системы (1) используют тот фундаментальный факт, что такие решения полностью определяются неподвижными точками оператора сдвига по траекториям системы. Однако использование данных теорем для непосредственного нахождения нужного периодического решения, скорее всего, не представляется возможным.
Читать полностью »
Эдвард Нортон Лоренц (1917 – 2008) является основателем теории хаоса, очень популярной в науке на сегодняшний день. Он учился в колледже Дартмут штата Нью-Гемпшир США и Гарвардском университете в Кембридже. Во время Второй мировой войны служил метеорологом в авиационном корпусе армии США, потом до конца своих дней работал профессором в Массачусетском технологическом институте.
В 1963 году в журнале «Journal of the Atmospheric Sciences» вышла его статья «Deterministic Nonperiodic Flow» (русский перевод: Лоренц Э. Детерминированное непериодическое течение // Странные аттракторы. — М.: Мир, 1981, с. 88-117), заложившая не только основы теории хаоса, но и изменившая представления о моделировании погодных явлений. В этой работе из системы уравнений Навье-Стокса впервые была получена нелинейная автономная система обыкновенных дифференциальных уравнений третьего порядка (динамическая система), описывающая движение воздушных потоков в плоском слое жидкости постоянной толщины при разложении скорости течения и температуры в двойные ряды Фурье с последующем усечением до первых-вторых гармоник:Читать полностью »
