План:
-
Вступление.
-
Логические операторы.
-
Четвертьсумматор.
-
Полусумматор.
-
Полный сумматор.
-
Заключение.
Вступление
Здравствуйте, в этой статье я подробно расскажу о том, как можно собрать свой собственный 4-битный сумматорЧитать полностью »

План:
Вступление.
Логические операторы.
Четвертьсумматор.
Полусумматор.
Полный сумматор.
Заключение.
Здравствуйте, в этой статье я подробно расскажу о том, как можно собрать свой собственный 4-битный сумматорЧитать полностью »
В целях недопущения злоупотеблениями я не указываю имя оператора.
Всё началось с того, что я купил по приезду SIM-карточку оператора с тарифным планом Pay-as-you-go. Это самый обычный тарифный план, которые были популярны в России до появления пакетных тарифных планов, то есть платишь за каждую минуту, сообщение, мегабайт, при этом у тебя есть баланс, который необходимо пополнять.
Читать полностью »

Китайская компания DJI, поставляющая на рынок разного рода беспилотные аппараты, разработала дрон-оператор. Это устройство может нести на себе видеокамеры и снимать с воздуха происходящее внизу. Правда, в отличие от всех прочих моделей коптеров, этот дрон, получивший название DJI Storm, не продается, зато его можно взять в аренду.
Насколько можно понять, вместе с дроном прилагается и команда операторов, дополнительных аксессуаров и грузовик, который может все это возить. Дрон позиционируется компанией как профессиональное устройство, предназначенное для киносъёмок.
Читать полностью »

В настоящее время сразу несколько российских операторов мобильной связи проводят тестирование технологии eSim. В число таких компаний входят, например, «Ростелеком» и Tele2.
Стоит отметить, что «Ростелком» работает как виртуальный сотовый оператор на сети Tele2. В ходе теста использовалось оборудование нескольких производителей. Все тесты завершены без проблем, настройки профиля оператора передавались на смартфон в автоматическом режиме.
Читать полностью »

Сегодня Госдума в третьем чтении приняла поправки в закон «О связи». Эти поправки отменяют национальный роуминг. Начиная с 1 июня следующего года операторы должны оказывать абонентам услуги по одинаковым тарифам — вне зависимости от того, в каком регионе России они находятся. Об этом сообщают «Ведомости».
Леонид Левин, председатель думского комитета по информационной политике, информационным технологиям и связи, заявил, что законопроект позволит отменить роуминг по всей России. Куда бы ни отправился абонент с сим-картой оператора, купленной в своем регионе, услуги для него будут предоставляться по тем же тарифам, что и в регионе покупки. Входящие звонки должны оставаться бесплатными.
Читать полностью »

Операторы федерального значения «ВымпелКом», «МегаФон» и МТС в ближайшее время планируют отменить плату за входящие звонки во внутрисетевом роуминге. Что касается «ВымпелКома» (бренд «Билайн»), то это случится не позже 20 августа. Таким образом, если абонент пользуется услугами связи в сети оператора, находясь за пределами «домашнего» региона, то платить не придется.
Сейчас за входящие вызовы абонент в национальном роуминге платит около 5 руб. за минуту разговора — в том случае, если вызов шел из иного региона, пишет «РБК». Информацию уже подтвердила пресс-секретарь компании «ВымпелКом» Анна Айбашева.
Читать полностью »
Ввиду того, что при решении задач оптимизации, дифференциальных игр, и в 2D и 3D расчётах, а вернее при написании софта, который проводит вычисления для их решения одними из наиболее часто выполняемых операций являются векторно-матричные преобразования типа 



Собственно вот такие:
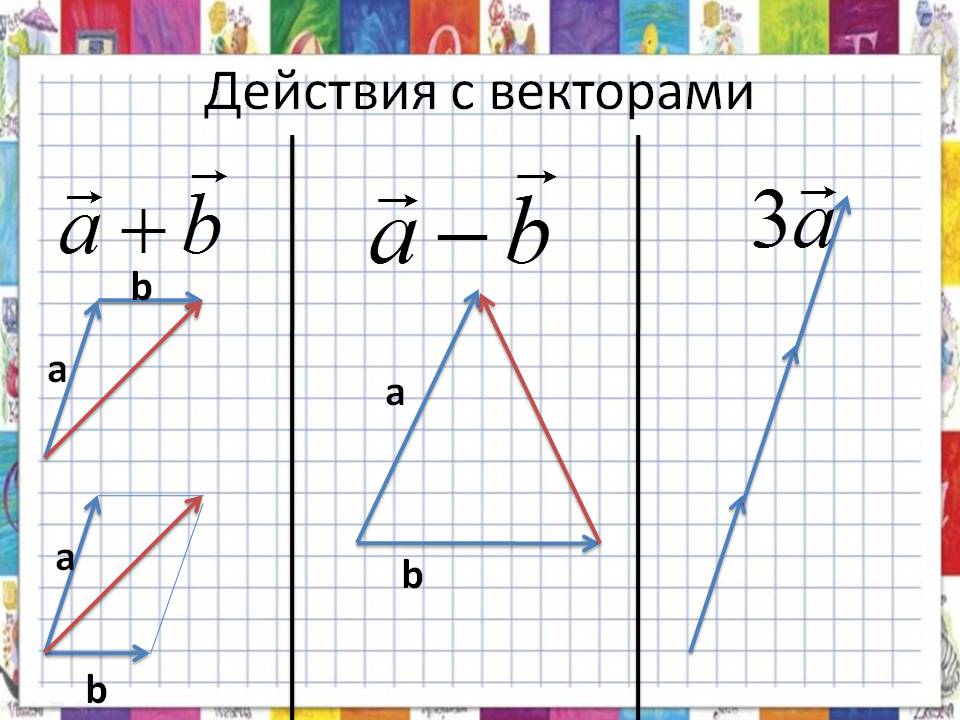
(источник).
Так, чтобы не углубляться в теорию оптимизации за примерами достаточно вспомнить формулу численного интегрирования Рунге-Кутты четвёртого порядка:
где 




Как можно заметить основную массу математических операций как для векторов, так и для матриц составляют:
О сложности вычислений хорошо написано в соответствующем курсе МФТИ.
Помимо этого, довольно существенные расходы при реализации векторных вычислений приходятся на операции управления памятью — создание и уничтожение массивов представляющих собой матрицы и вектора.
Соответственно есть смысл заняться снижением количества операций привносящих наибольшую сложность — умножения (математика) и операции управления памятью (алгоритмика).

Исследовательская компания «ТМТ консалтинг», проанализировав тарифные планы большинства российских провайдеров, предоставляющих услуги подключения к сети интернет по кабелю, сделала вывод о постепенном подорожании фиксированного интернета в Регионах РФ. Архивные тарифы, которые давали пользователям возможность экономить, закрываются, абоненты переводятся на новые, более дорогие тарифы, пишут «Ведомости». Раньше стоимость минимального тарифного плана составляла примерно 300 руб. в месяц. Сейчас цена выросла до 400 рублей.
Правда, до заметного повышения среднего ежемесячного счета (ARPU) пока не дошло. В июле-сентябре рост счета по сравнению с предыдущим кварталом составил всего 1 руб. Год назад этот показатель составлял 338 руб, то есть рост есть, но пока он минимальный. Ситуация могла бы быть еще более заметной, если бы «Вымпелком» не предлагал тариф «Все в одном», когда пользователям мобильной связи оператора доступна и услуга проводного интернета.
Читать полностью »
Недавно ФАС предписало операторам отменить роуминг, и дала на это дело 2 недели. Операторы офигели и ничего не сделали, соответственно разразился хайп по поводу того, какие же они бяки. И, в общем, операторы не белые и не пушистые, но всё-таки не такие плохие, как можно считать.
В этой статье я хочу объяснить, какие есть проблемы, и почему 2 недели — это популистский наезд а не реальное желание решить проблему глобально.
Читать полностью »