Продолжаем традицию подробных отчетов о финалах RCC (прошлогодний аналогичный пост — здесь). Итак, 23 сентября 2013 года завершился третий чемпионат по спортивному программированию — Russian Code Cup 2013. Первое место занял Петр Митричев, повторив собственное достижение 2011 года, второе — Геннадий Короткевич, победивший в этом году вместе с командой ИТМО в финале ACM ICPC в Санкт-Петербурге. Третьим стал Дмитрий Джулгаков, уже третий раз участвовавший в финале чемпионата, но впервые завоевавший призовое место.
Рубрика «олимпиадное программирование» - 3
Финал чемпионата по программированию Russian Code Cup: как это было
2013-10-07 в 10:18, admin, рубрики: mail.ru, rcc, Russian Code Cup, Блог компании Mail.Ru Group, олимпиадное программирование, Программирование, Спортивное программирование, метки: mail.ru, rcc, Russian Code Cup, олимпиадное программирование
Финал RussianCodeCup 2013: Фоторепортаж
2013-09-30 в 4:39, admin, рубрики: rcc, олимпиадное программирование, Программирование, метки: rcc, олимпиадное программирование, Программирование Друзья, если вы не попали на финал RussianCodeCup 2013, не отчаивайтесь, мы расскажем о всём самом интересном.
Если вы были с нами, у вас есть возможность освежить воспоминания и поделиться в комментариях впечатлениями.
Задачка из реальной жизни: Как восстановить дерево процессов в Linux
2013-09-26 в 9:57, admin, рубрики: algorithms, CRIU, linux, system programming, Алгоритмы, олимпиадное программирование, олимпиадные задачи, системное программирование, Спортивное программирование, метки: algorithms, CRIU, linux, system programming, олимпиадное программирование, олимпиадные задачиМы разрабатываем проект CRIU (Checkpoint/Restore in Userspace) и у нас возникла достаточно интересная задача о том, как восстановить оригинальное дерево процессов. Я предлагаю вам попытаться решить ее.
Задача
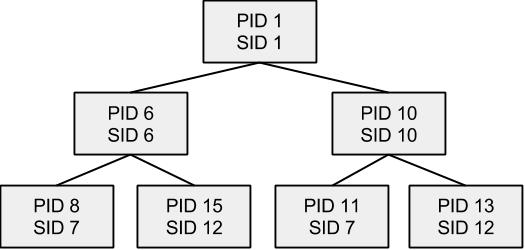
CRIU — это утилита, которая позволяет сохранить состояние процессов на диск и постановить их позднее на этой или на любой другой машине. Одной из подзадач восстановления является нахождение последовательности действий для того, чтобы восстановить дерево процессов. Входные данные содержат набор параметров для каждого процесса: уникальный идентификатор (PID), ссылку на родителя (PPID), идентификатор сессии (SID).
Заочная олимпиада по спортивному программированию для школьников от НИТУ МИСиС и Cognitive Technologies
2013-09-25 в 7:41, admin, рубрики: cognitive technologies, Блог компании Cognitive Technologies, олимпиадное программирование, Спортивное программирование, школьники, метки: cognitive technologies, олимпиадное программирование, спортивное программирование, школьникиПривет!
Этой осенью для школьников будет проходить заочная олимпиада по спортивному программированию от МИСиС и компании Cognitive Technologies. Приглашаются учащиеся 9-11 классов из любых российских школ.
Призер всероссийской олимпиады по информатике задержан во время взлома банкомата
2013-07-11 в 3:39, admin, рубрики: взлом, информационная безопасность, олимпиадное программирование, Программирование, Спортивное программирование, метки: взлом, олимпиадное программирование, ПрограммированиеПродолжаем интересные новости: в Иркутске задержан студент-первокурсник, серебряный призер всероссийской олимпиады по информатике. Арест произошел в том момент, когда 19-ти летний парень пытался украсть около 75 тысяч рублей, снимая деньги и переводя их на телефонные счета. Влом произошел в одном из продуктовых магазинов Иркутска. Охранники обратили внимание на молодого человека, который долгое время производил подозрительные манипуляции у терминала, находящегося в помещении магазина. Ну и вызвали полицию.
Цитирую пресс-службу МВД:Читать полностью »
Олимпиада по программированию Летней школы МФТИ по прикладным математике и физике
2013-07-03 в 5:54, admin, рубрики: абитуриентам, интересные задачи, летняя школа МФТИ, МФТИ, ненормальное программирование, олимпиадное программирование, Программирование, Спортивное программирование, метки: абитуриентам, интересные задачи, летняя школа МФТИ, МФТИ, олимпиадное программирование В настоящее время для абитуриентов МФТИ проводится школа по прикладным математике и физике (подробнее о ней можно прочитать на официальном сайте). В её рамках на сайте http://judge.mipt.ru/index_school.html проходит заочная олимпиада по программированию. Она проводится по кировской системе (то есть баллы приносит
Читать полностью »
Как побеждают IT-чемпионы: про изнанку подготовки к ACM-ICPC
2013-07-02 в 12:22, admin, рубрики: Russian Code Cup, Блог компании Mail.Ru Group, олимпиадное программирование, олимпиады по программированию, Программирование, Спортивное программирование, метки: ACM ICPC, Russian Code Cup, олимпиадное программирование, олимпиады по программированию1- 3 июля 2013 в Санкт-Петербурге проходит финал Международной студенческой олимпиады по спортивному программированию ACM-ICPC. Решающая встреча джедаев спортивного программирования пройдет в городе на Неве благодаря тому, что студенты питерского ИТМО заняли первое место на ACM-ICPC 2012.
Mail.Ru Group давно сотрудничает с ИТМО: там действует наша кафедра интернет-технологий, там же по нашему приглашению Бертран Майер возглавил кафедру программной инженерии, мы неоднократно становились партнерами этапов и полуфиналов ACM и совместно проводим собственный чемпионат по спортивному программированию Russian Code Cup. Поэтому мы решили дополнительно поддержать команду ИТМО в преддверии ответственного финала, и прежде всего – рассказать о чемпионах :)
Russian Code Cup 2013 – разбор задач отборочного раунда
2013-06-20 в 7:48, admin, рубрики: rcc, Блог компании Mail.Ru Group, олимпиадное программирование, Программирование, разбор задач, Спортивное программирование, метки: rcc, олимпиадное программирование, разбор задач 
В прошедшее воскресенье состоялся отборочный раунд Russian Code Cup. Это последний онлайн-раунд соревнования: решающая встреча финалистов пройдет в Москве. Для того чтобы участвовать в финале, нужно было приложить больше усилий, чем на предыдущих этапах. Участникам предлагалось шесть задач (в квалификационных раундах было на одну меньше), на их решение выделялось три часа (в квалификационных — два).
Борьба за выход в финал была непростой, но честной: за время раунда не выявлено ни одного списывальщика.
Под катом — статистика по победителям и подробный разбор задач отборочного раунда:
- Задача A: Две башни
- Задача B: Депозит
- Задача C: Кеплер
- Задача D: Тест
- Задача E: Лазеры
- Задача F: Колесо
Школьник об олимпиадном программировании
2013-04-29 в 10:29, admin, рубрики: олимпиадное программирование, Спортивное программирование, метки: олимпиадное программирование, спортивное программирование 
Здравствуй!
Пишет тебе девятиклассник, призер регионального этапа всероссийской олимпиады по информатике. В последнее время я стал замечать, что у читателей повысился интерес к олимпиадам по программированию. Как их активный участник я постараюсь ответить на все вопросы, рассказать о своем пути, привести примеры реальных, запомнившихся мне задач.
Читать полностью »
Олимпиадные задачи по программированию: что за зверь?
2013-04-11 в 20:11, admin, рубрики: Блог компании ABBYY, олимпиадное программирование, Спортивное программирование, метки: олимпиадное программирование, спортивное программирование 
Недавно мы анонсировали конкурс задач по спортивному программированию. Организаторы конкурса попросили написать короткое объявление о конкурсе в блог, но строгий редактор отказался печатать анонс без объяснения того, что же такое олимпиадная задача. Из этого родилась целая статья. Начнем, пожалуй, с примера олимпиадной задачи.
Этот же пример, чтобы по ссылке не ходить
ИТ-рестораны
ограничение по времени на тест: 4 секунды
ограничение по памяти на тест: 256 мегабайт
ввод: standard input
вывод: standard output
В городе N. очень плохо с дорогами, общепитом и IT-инфраструктурой. Всего в городе n перекрестков, некоторые пары которых соединены двусторонними дорогами. Дорожная сеть состоит из n - 1 дороги, по дорогам можно добраться с любого перекрестка на любой другой. Да, вы правы — дорожная сеть образует неориентированное дерево.
Недавно мэр города придумал способ, устраняющий проблемы с общепитом и IT-инфраструктурой, причем одновременно! Решено поставить на перекрестках города ресторанчики двух известных сетей кафе для IT-шников: «iMac D0naldz» и «Burger Bing». Так как владельцы сетей не дружат, категорически запрещается размещать рестораны двух разных сетей на соседних перекрестках. Есть и другие требования. Вот полный список:
- в каждом перекрестке должен находится не более чем один ресторан;
- каждый ресторан принадлежит либо «iMac D0naldz», либо «Burger Bing»;
- каждая сеть должна построить не менее одного ресторана;
- не существует пары перекрестков, которые соединены дорогой и на которых стоят рестораны разных сетей.
Мэр собирается брать неплохой налог с каждого ресторана, поэтому он заинтересован в том, чтобы общее число ресторанов было максимальным.
Помогите мэру проанализировать ситуацию. Найдите все такие пары (a, b), что a ресторанов может принадлежать «iMac D0naldz», b — «Burger Bing», а сумма a + b максимальна.
Входные данные
В первой строке входных данных содержится целое число n (3 ≤ n ≤ 5000) — количество перекрестков в городе. Далее в n - 1 строке перечислены все дороги, по одной дороге в строке. Каждая дорога задана парой чисел xi, yi (1 ≤ xi, yi ≤ n) — номерами соединяемых перекрестков. Считайте, что перекрестки пронумерованы от 1 до n.
Гарантируется, что заданная дорожная сеть представляет собой неориентированное дерево с n вершинами.
Выходные данные
В первую строку выведите целое число z — количество искомых пар. Далее выведите все искомые пары (a, b) в порядке увеличения первой компоненты a.
Примеры тестов
Входные данные
5
1 2
2 3
3 4
4 5
Выходные данные
3
1 3
2 2
3 1
Входные данные
10
1 2
2 3
3 4
5 6
6 7
7 4
8 9
9 10
10 4
Выходные данные
6
1 8
2 7
3 6
6 3
7 2
8 1
Первое, что бросается в глаза, это необычное условие. Такой подход сложился исторически: писать краткую математическую формулировку не принято. Обычно ее пытаются связать с реальной жизнью, ну или с не очень реальной. Например, в USACO героями всех задач являются фермер Джон и коровы. Прежде чем приступить к решению после прочтения условия, участнику требуется выделить математическую формулировку задачи.
Читать полностью »