Рубрика «нерешенная проблема»

Задача о хроматическом числе плоскости формулируется следующим образом: в какое наименьшее число цветов можно раскрасить плоскость так, чтобы любые две точки на расстоянии 1 были покрашены в различные цвета?

Эту задачу сформулировали Хуго Хадвигер и Пал Эрдёш в сороковых годах XX века. Независимо от них примерно в то же самое время этой задачей занимались Эдуард Нелсон и Дж. Р. Исбелл. После работы Хадвигера 1961 года об открытых на тот момент проблемах, хроматическое число плоскости стало активно изучаться.

Сразу же было показано, что в 3 цвета плоскость требуемым образом раскрасить нельзя, однако 7 цветов достаточно. Действительно, легко выбрать на плоскости несколько точек так, что некоторые из них находятся на расстоянии ровно 1 (такая конструкция точек называется графом единичных расстояний), и затем перебором показать, что в 3 цвета эти точки раскрасить невозможно. Примеры таких графов — веретено Мозера и граф Голомба приведены на картинке ниже. Чтобы показать, что 7 цветов достаточно, замостим плоскость правильными шестиугольниками со стороной 0.4 и закрасим их по определенному паттерну, как на картинке ниже. Тогда, как несложно убедиться, концы любого отрезка длины 1 будут лежать в разных шестиугольниках различных цветов.

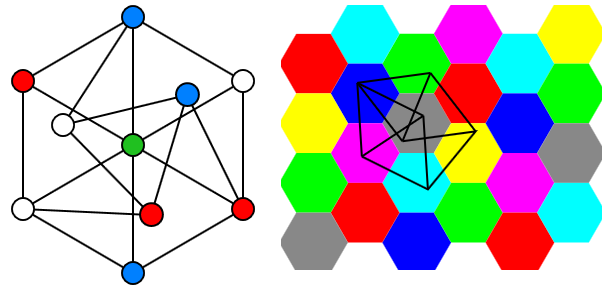
Однако, с тех пор никто не мог уточнить ни верхнюю, ни нижнюю границы. Задача получила название Проблема Нелсона — Эрдёша — Хадвигера. Прошло 60 лет, и вот, в апреле 2018 года математик-любитель Обри де Грей предъявил граф единичных расстояний, который нельзя покрасить в 4 цвета.
Читать полностью »