Данный пост является продолжением моей статьи [1] на Хабрахабре об аттракторе Лоренца. Здесь рассмотрим метод построения приближенных решений соответствующей системы, уделив внимание программной реализации.
Динамической системой Лоренца является автономная система обыкновенных дифференциальных уравнений третьего порядка
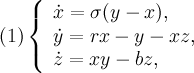
где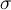 
, r и b являются положительными числами. Для исследования поведения решений системы обычно берут классические значения параметров системы, т.е.
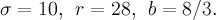
Как было отмечено в статье [1], в этом случае в системе (1) имеет место неустойчивость ее решений на аттракторе. По сути, это делает некорректным применение классических численных методов на больших отрезках времени (а на таких отрезках и строятся притягивающие множества динамических систем). Одним из вариантов преодоления этой проблемы является переход к высокоточным вычислениям, но такой подход ставит исследователя в жесткие рамки: во-первых, малая степень свободы для уменьшения ошибки (изменение величины шага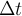 
интегрирования и точности представления вещественного числа для управления вычислительным процессом), во-вторых, большой объем вычислений при очень малых 
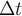.Читать полностью »