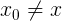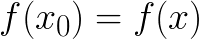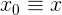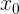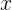В статье приводится новое доказательство красивой и трудной теоремы математического анализа, изложенное таким образом, что оно доступно учащимся старших классов профильных математических школ.
Пусть
— бесконечно много раз дифференцируемая действительная функция, причем для каждой точки
найдется натуральное
такое, что
. Тогда
многочлен.
Доказательство
Нам понадобится теорема Бэра о системе замкнутых множеств:
1. Пусть
и
замкнутые подмножества прямой, причем
и
. Тогда в
найдется точка, которая содержится в одном из
вместе со своей окрестностью. Более точно, найдется точка
, натуральное
и
такие, что
.
Действительно (от противного), выберем точку 

















Так как каждый промежуток 





Скажем, что точка на действительной прямой правильная, если в некоторой окрестности этой точки функция  — многочлен. Множество всех правильных точек обозначим символом — многочлен. Множество всех правильных точек обозначим символом  . Множество . Множество  , дополнительное к , дополнительное к  обозначим через обозначим через  и назовем множеством неправильных точек. (Будем говорить, что если и назовем множеством неправильных точек. (Будем говорить, что если  , то , то  — неправильная точка). — неправильная точка). |
|---|