Итак, очередная статья из цикла «математика на пальцах». Сегодня мы продолжим разговор о методах наименьших квадратов, но на сей раз с точки зрения программиста. Это очередная статья в серии, но она стоит особняком, так как вообще не требует никаких знаний математики. Статья задумывалась как введение в теорию, поэтому из базовых навыков она требует умения включить компьютер и написать пять строк кода. Разумеется, на этой статье я не остановлюсь, и в ближайшее же время опубликую продолжение. Если сумею найти достаточно времени, то напишу книгу из этого материала. Целевая публика — программисты, так что хабр подходящее место для обкатки. Я в целом не люблю писать формулы, и я очень люблю учиться на примерах, мне кажется, что это очень важно — не просто смотреть на закорючки на школьной доске, но всё пробовать на зуб.
Итак, начнём. Давайте представим, что у меня есть триангулированная поверхность со сканом моего лица (на картинке слева). Что мне нужно сделать, чтобы усилить характерные черты, превратив эту поверхность в гротескную маску?
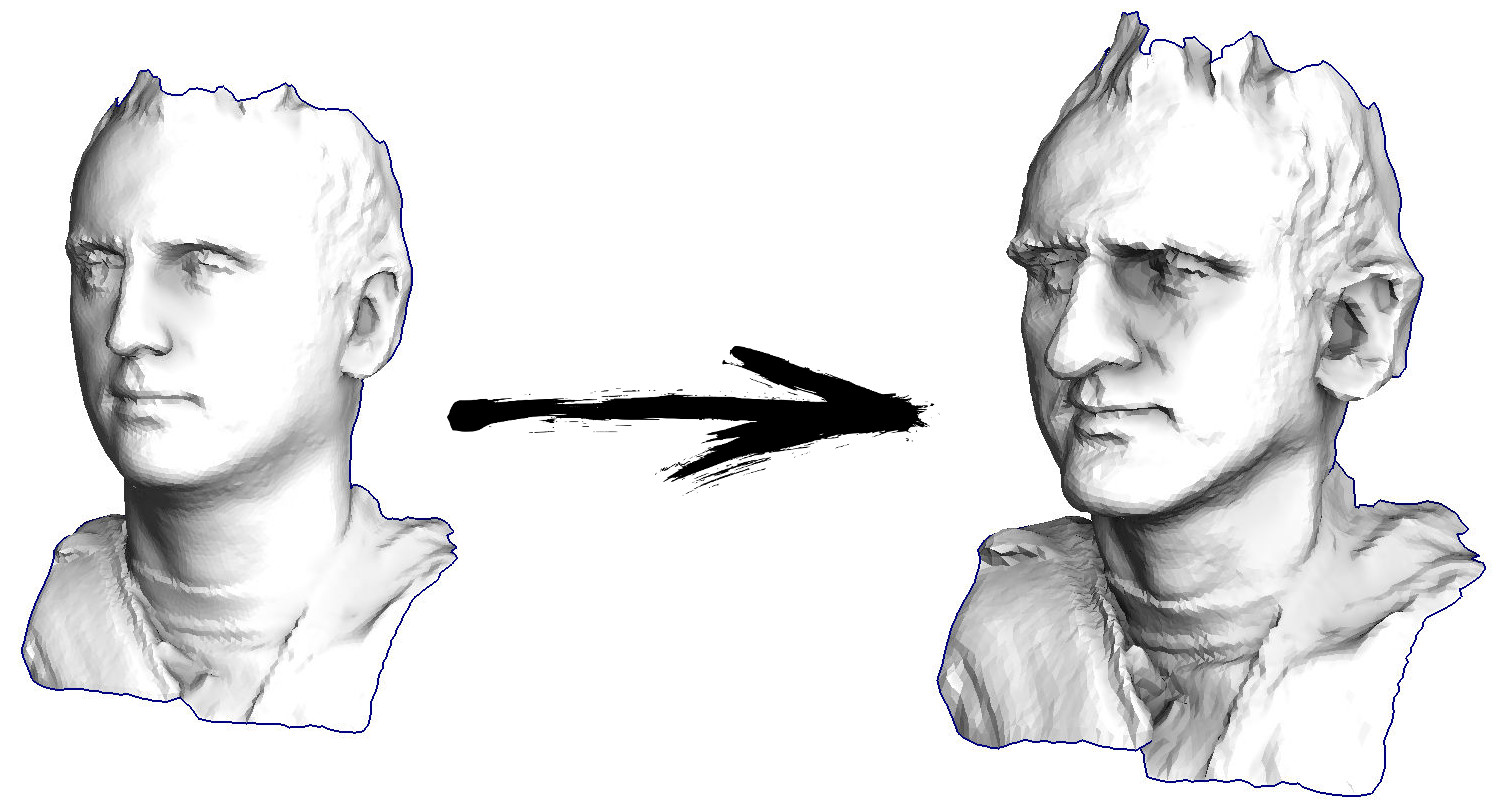
В данном конкретном случае я решаю эллиптическое дифференциальное уравнение, носящее имя Симеона Деми Пуассона. Товарищи программисты, давайте сыграем в игру: прикиньте, сколько строк в C++ коде, его решающем? Сторонние библиотеки вызывать нельзя, у нас в распоряжении только голый компилятор. Ответ под катом.

