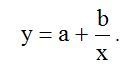Рубрика «метод наименьших квадратов»

в 10:53, , рубрики: data mining, Алгоритмы, дрейф нуля, математика, метод наименьших квадратов, препроцессинг данных, стационарный процесс, тренд, удаление тренда

При анализе экспериментально полученных стационарных временных рядов, как правило, при предварительной подготовке (препроцессинге) данных возникает необходимость в подавлении имеющегося в них тренда.
Здесь будет предложен «новый» метод выделения тренда — простой, очевидный и пригодный для очень сложных видов тренда.

Под трендом обычно понимают сверхнизкочастотную негармоническую компоненту, резко нарушающую стационарность процесса. Наиболее частой причиной тренда в экспериментально полученных данных является «дрейф нуля» регистрирующей аппаратуры. Интегрирование данных и некоторые другие виды обработки также могут стать причиной появления тренда. Наличие тренда сильно искажает результаты последующей обработки данных (спектральное оценивание и т.п.), поэтому удаление тренда является необходимым. В ряде случаев сам тренд является ценным источником информации (например, при анализе долгосрочных тенденций в экономических или метео- процессах).
image
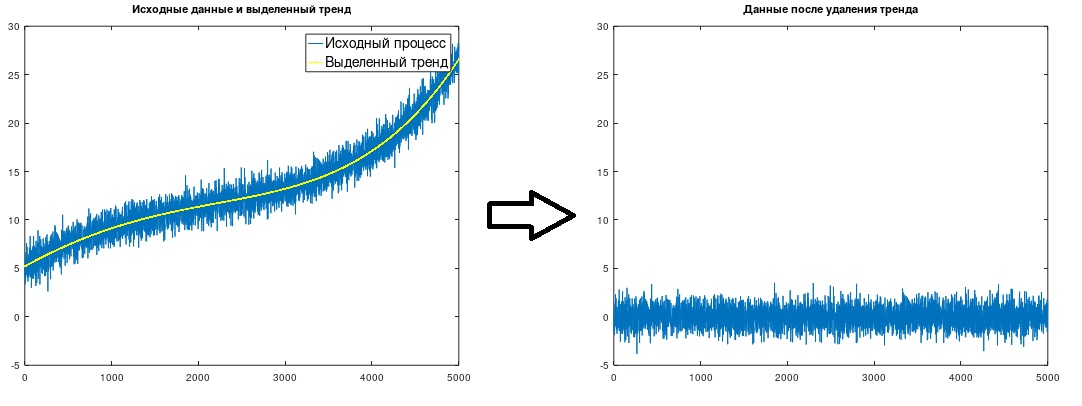
Рис. 1. Выделение и удаление тренда.
Читать полностью »

в 8:21, , рубрики: python, аппроксимация, метод наименьших квадратов

Зачем это нужно

Законы Зипфа оописывают закономерности частотного распределения слов в тексте на любом естественном языке[1]. Эти законы кроме лингвистики применяться также в экономике [2]. Для аппроксимации статистических данных для объектов, которые подчиниться Законам Зипфа используется гиперболическая функция вида:

Простая программа на Python для гиперболической аппроксимации статистических данных - 1(1)

где: a.b – постоянные коэффициенты: x – статистические данные аргумента функции (в виде списка): y- приближение значений функции к реальным данным полученным методом наименьших квадратов[3].

Обычно для аппроксимации гиперболической функцией методом логарифмирования её приводят к линейной, а затем определяют коэффициенты a,b и делают обратное преобразование [4]. Прямое и обратное преобразование приводит к дополнительной погрешности аппроксимации. Поэтому привожу простую программу на Python, для классической реализации метода наименьших квадратов.Читать полностью »

в 16:16, , рубрики: curve-fitting, data mining, Алгоритмы, математика, машинное обучение, метод наименьших квадратов, методы оптимизации

Алгоритм Левенберга — Марквардта для нелинейного метода наименьших квадратов и его реализация на Python - 1

Нахождение экстремума (минимума или максимума) целевой функции является важной задачей в математике и её приложениях (в частности, в машинном обучении есть задача curve-fitting). Наверняка каждый слышал о методе наискорейшего спуска (МНС) и методе Ньютона (МН). К сожалению, эти методы имеют ряд существенных недостатков, в частности — метод наискорейшего спуска может очень долго сходиться в конце оптимизации, а метод Ньютона требует вычисления вторых производных, для чего требуется очень много вычислений.

Для устранения недостатков, как это часто бывает, нужно глубже погрузиться в предметную область и добавить ограничения на входные данные. В частности: МНС и МН имеют дело с произвольными функциями. В статистике и машинном обучении часто приходится иметь дело с методом наименьших квадратов(МНК). Этот метод минимизирует сумму квадрата ошибок, т.е. целевая функция представляется в виде:

Алгоритм Левенберга — Марквардта для нелинейного метода наименьших квадратов и его реализация на Python - 2

Алгоритм Левенберга — Марквардта используется для решения нелинейного метода наименьших квадратов. Статья содержит:

  • объяснение алгоритма
  • объяснение методов: наискорейшего спуска, Ньтона, Гаусса-Ньютона
  • приведена реализация на Python с исходниками на github
  • сравнение методов

Читать полностью »

в 20:40, , рубрики: c++, lqr, Алгоритмы, ардуино головного мозга, линейно-квадратичный регулятор, математика, математика на пальцах, метод наименьших квадратов, программирование микроконтроллеров, Разработка робототехники

Постановка задачи: как со школьными знаниями дойти до выводов университетского уровня

Эта статья предполагает, что вы прочли мои статьи (ну или и без того знаете) про методы наименьших квадратов и про линейно-квадратичный регулятор.

Как я уже говорил в предыдущих статьях, мои знакомые студенты хотят построить обратный маятник, но умаялись подбирать коэффициенты ПИД-регулятора, поэтому я неспешно смотрю, что такое линейно-квадратичный регулятор, ну а заодно и вам пересказываю то, что прочитал. Задача для этой статьи — показать, как воплотить в железе одномерный пример из статьи про линейно-квадратичный регулятор. Грубо говоря, я хочу написать написать управление для сервомотора: у меня есть текущее положение оси привода и текущая скорость её вращения, я хочу её остановить в заданном положении. Я попытался было прочитать схожую статью на эту тему, но, признаться, ничего в ней не понял, поэтому сел разбираться самостоятельно, предпочтительно на пальцах и без страшных слов типа дифференциальных уравнений Лагранжа-Эйлера.

Продолжая рабочий эксгибиционизм, знакомлю вас с Bubble Bobble, который живёт у нас с коллегой в кабинете. Он рецензирует статьи для конференции SIGGRAPH.

Математика на пальцах: ардуино головного мозга или линейно-квадратичный регулятор для управлением электродвигателем - 1

Читать полностью »

в 19:06, , рубрики: machine learning, statistical learning, Блог компании Нерепетитор.ру, визуализация данных, конверсия сайтов, корреляция, линейная регрессия, математика, математика и реальная жизнь, машинное обучение, метод наименьших квадратов, монте-карло, статистика

Как и обещал, начинаю цикл статей по «машинному обучению». Эта будет посвящена таким понятиям из статистики, как корреляция случайных величин и линейная регрессия. Рассмотрим, как реальные данные, так и модельные (симуляцию Монте-Карло).

Часть 1. Реальные данные

Чтобы было интереснее, рассказ построен на примерах, причем в качестве данных (и в этой, и в следующих, статьях) я буду стараться брать статистику прямо отсюда, с Хабра. А именно, неделю назад я написал свою первую статью на Хабре (про Mathcad Express, в котором и будем все считать). И вот теперь статистику по ее просмотрам за 10 дней и предлагаю в качестве исходных данных. На графике это ряд Views, синяя линия. Второй ряд данных (Regs, с коэффициентом 100) показывает число читателей, выполнивших после прочтения определенное действие (регистрацию и скачивание дистрибутива Mathcad Prime).

Машинное обучение — 1. Корреляция и регрессия. Пример: конверсия посетителей сайта - 1
Читать полностью »

Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js