Сегодня мы рассмотрим графический пакет для языка Julia, который называется Luxor. Это один из тех инструментов, которые превращают процесс создания векторных изображений в решение логических задачек с сопутствующей бурей эмоций.
Осторожно! Под катом 8.5 Мб легковесных картинок и гифок изображающих психоделические яйца и четырехмерные объекты, просмотр которых может вызвать лёгкое помутнение рассудка!
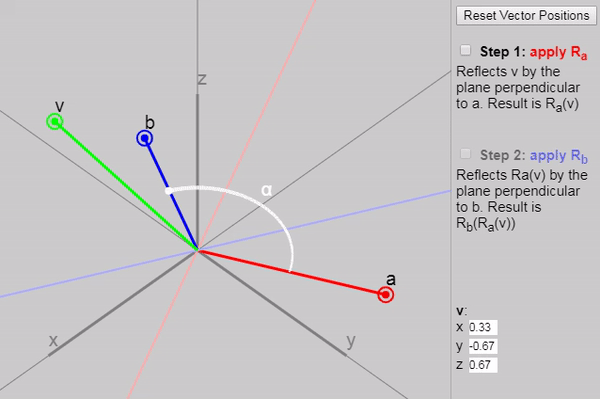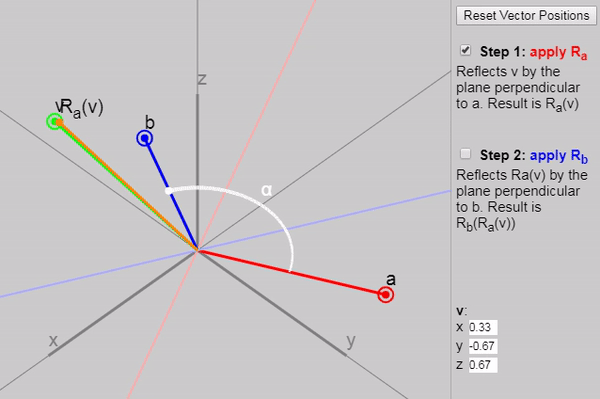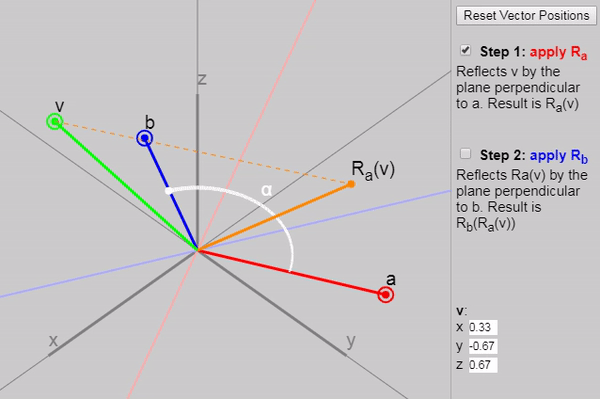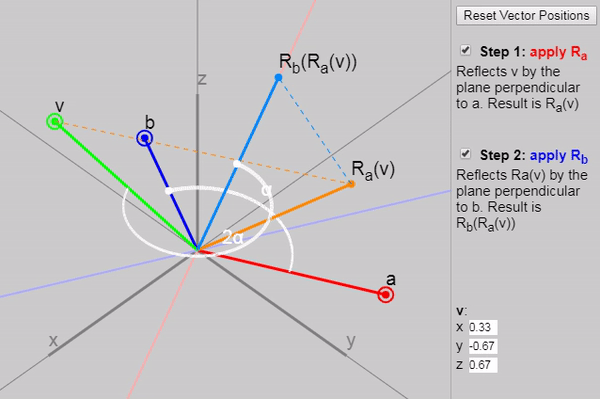
Для записи трёхмерных поворотов программисты графики используют кватернионы. Однако в кватернионах сложно разобраться, потому что изучают их поверхностно. Мы просто принимаем на веру странные таблицы умножения и другие загадочные определения, и используем их как «чёрные ящики», поворачивающие векторы так, как нам нужно. Почему 
и 
? Почему мы берём вектор и превращаем его в «мнимый» вектор, чтобы преобразовать его, например 
? Да кому это интересно, если всё работает, правда?
Существует способ описания поворотов под названием ротор, который относится к области и комплексных чисел (в 2D), и кватернионов (в 3D), и даже обобщается до любого количества измерений.
Мы можем создавать роторы практически полностью с нуля, вместо того, чтобы определять из ничего кватернионы и пытаться объяснить, как они работают задним числом. Это занимает больше времени, но мне кажется, что это стоит того, потому что их гораздо легче понять!
Кроме того, для визуализации и понимания трёхмерных роторов не нужно использовать четвёртое пространственное измерение.
Было бы здорово, если бы начали вытеснять использование и изучение кватернионов, заменяя их роторами. Заменить их очень просто, а код останется почти таким же. Всё, что можно делать с кватернионами, например, интерполяцию и устранение блокировки осей (Gimbal lock), можно сделать и с роторами. Но понимать мы начинаем гораздо больше.
Читать полностью »
При решении задач моделирования движения объектов в трехмерном пространстве практически всегда требуется использование операций пространственных преобразований, связанных с умножением матриц преобразований и векторов. Для задачи N тел эта операция используется многократно для задания поворота и смещения тела относительно начала координат. Матрица пространственного преобразования имеет размерность 4х4, а размерность вектора, к которому применяется преобразование, соответственно 4x1. Рассмотрим оптимизацию выполнения такой операции с большим числом матриц и векторов под архитектуру Intel® Xeon Phi™.
