Матричное расширение (instruction set architecture) — это часть архитектуры компьютера, которая определяется программируемой частью ядра микропроцессора.</p>" data-abbr="ISA">ISA CPU… Что это и что оно делает? Уже из названия понятно, что это расширение позволяет ускорять операции над матрицами на CPU. Но задумывались ли вы когда-нибудь, какие они бывают, когда появились, кто и как их создает?
Рубрика «матрицы»
Панорама матричных расширений: от x86 до RISC-V
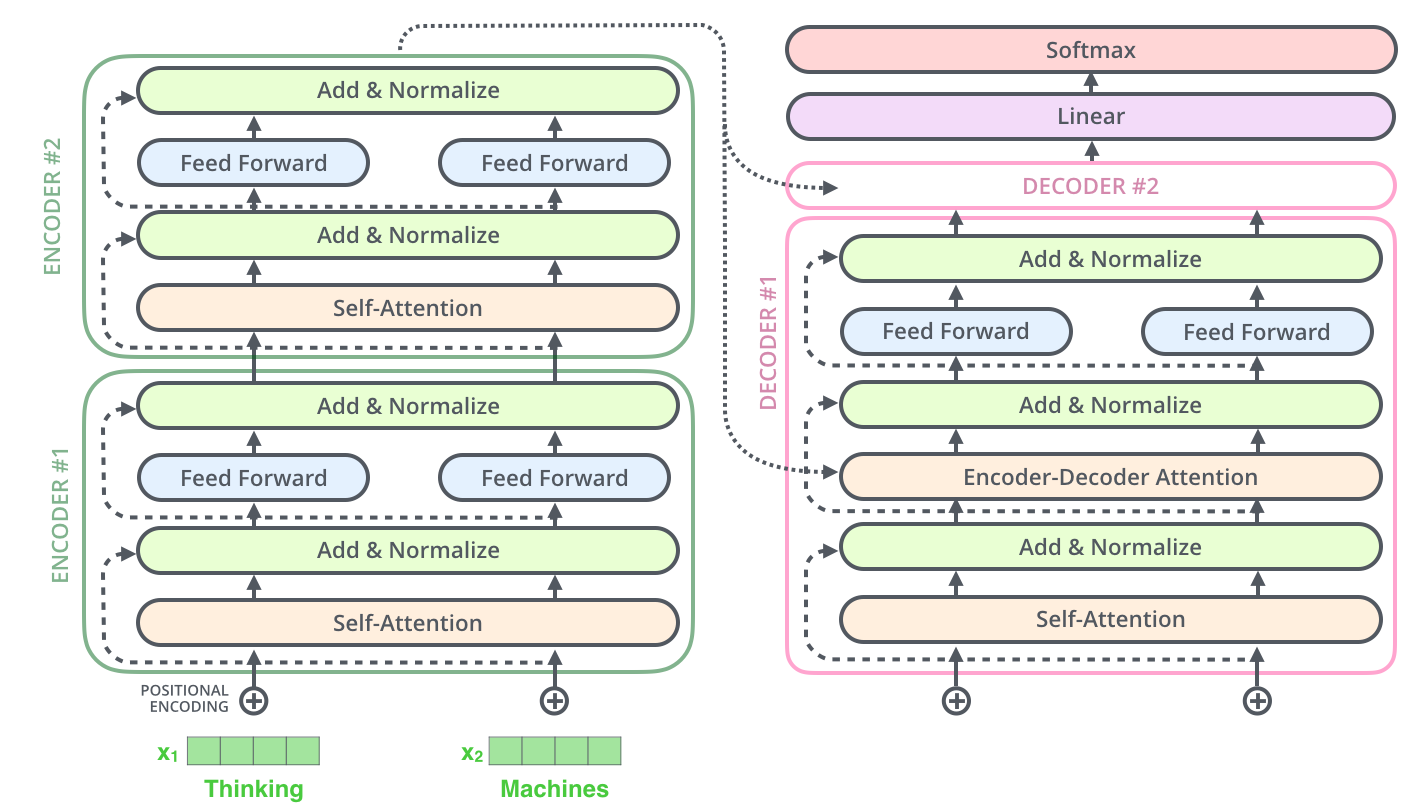
2024-07-09 в 14:17, admin, рубрики: cpu, HPC, ISA, matrix, risc-v, матрицы, Матричные расширения, операцииКак работают трансформеры: разбираем математику
2024-01-18 в 7:16, admin, рубрики: chatgpt, Transformers, матрицы, трансформеры
Подключаем дисплей к любому одноплатнику с SPI: большой мануал о поиске экранчиков для ваших проектов
2023-08-14 в 8:01, admin, рубрики: bodyawm_ништячки, C, DIY, diy или сделай сам, lcd, Orange Pi, SPI, timeweb_статьи, Блог компании Timeweb Cloud, дисплеи, матрицы, одноплатники, одноплатные компьютеры, Разработка под Linux
Сейчас появилось достаточно много различных дешевых одноплатников с очень достойными характеристиками, которые вполне можно назвать экономичными и портативными. Однако очень часто встает вопрос вывода изображения на дисплей: к сожалению, в подобные устройства обычно ставят урезанные версии чипсетов без видеовыхода на обычные матрицы. Конечно в них практически всегда есть HDMI, но это совершенно не выход для портативного устройства: прожорливый чип скалера будет очень негативно влиять на время работы от АКБ. Да и сами подобные дисплеи очень дорогие: почти 2.000 рублей за матрицу со скалером — это действительно бьет по карману. Сегодня я расскажу Вам о существующих протоколах для дисплеев, подскажу, как применить экранчики от старых навигаторов/мобильников и мы подключим с вами SPI-дисплей к одноплатнику без видеовыхода. Причем мы реализуем как просто библиотеку, которая позволяет выводить произвольную графику из ваших программ, так
и службу, которая будет напрямую копировать данные из фреймбуфера и преобразовывать в формат для нашего дисплея. Интересно? Тогда жду вас в статье!Читать полностью »
Как эволюция матриц цифровых камер помогает нейрофизиологам изучать эпилепсию
2022-12-16 в 10:02, admin, рубрики: биология, Блог компании FirstVDS, матрицы, мозг, мозг-компьютер, мыши, наука и техника, наука и технологии, Научно-популярное, нейронные сети, чипы, эпилепсия
Источник: здесь
Я люблю эволюцию, люблю наблюдать и пытаться осмыслить ее проявления в самых разных областях нашей реальности. По первоначальному образованию инженер, я, волей судьбы, с большим удовольствием и интересом занимаюсь изучением эпилепсии в аспирантуре Кёльнского Университета.Читать полностью »
Как я снял спутники Юпитера на ТЕЛЕФОН
2021-09-16 в 20:35, admin, рубрики: астрономия, матрицы, Научно-популярное, планеты, смартфоны, спутники, Фототехника, юпитерПеред вами первая (в истории?) фотография Юпитера и его спутников, сделанная на ТЕЛЕФОН без использования дополнительных оптических средств, таких как телескоп или внешние объективы. Только штатив, только хардкор.
Матричное умножение. Медленное достижение мифической цели
2021-03-28 в 12:01, admin, рубрики: timeweb, Блог компании TIMEWEB, математика, матрицы, метод штрассена, Научно-популярное, умножения матрицВ недавней работе был установлен новый рекорд скорости по умножению двух матриц. Она также знаменует и конец эпохи для метода, который ученые применяли для исследований на протяжении десятилетий.
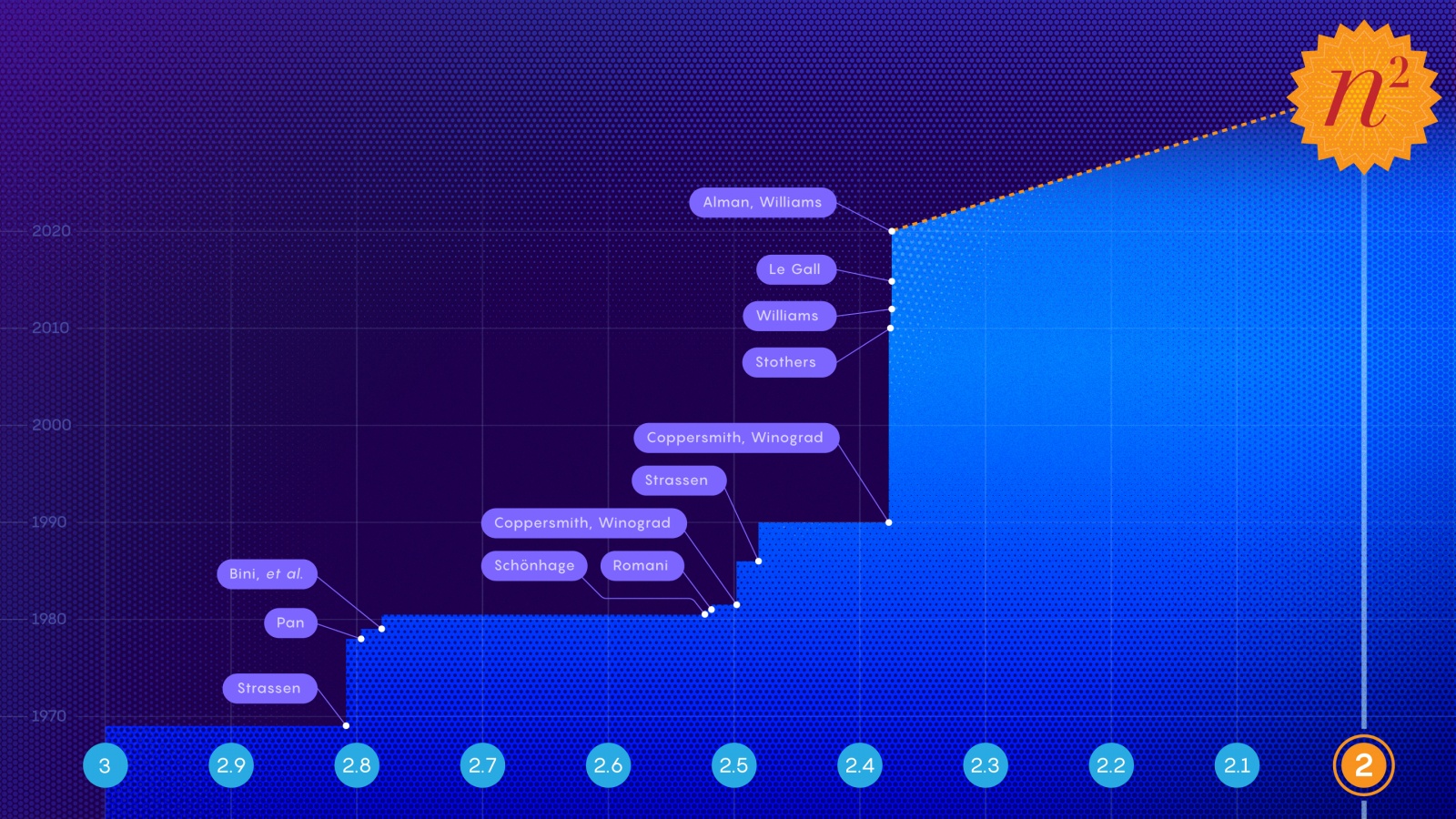
Математики стремятся к достижению мифической цели — второй степени (exponent two), то есть к умножению пары матриц n х n всего за n2 шагов. Исследователи подбираются все ближе к своей цели, но получится ли у них когда-нибудь достичь ее?
Читать полностью »
«Бесполезное» представление, преобразовавшее математику
2020-06-23 в 11:00, admin, рубрики: группы, математика, матрицы, Научно-популярное, теория представленийИзначально от теории представлений отказались. Сегодня она играет важнейшую роль в большинстве областей математики.
Когда в конце XIX века впервые появилась теория представлений, многие математики сомневались в ценности этого подхода. В 1897 году английский математик Уильям Бёрнсайд писал, что сомневается в том, что эта необычная перспектива даст какие-то полезные результаты.
«Бёрнсайд, по сути, говорил о том, что теория представлений бесполезна», — сказал Джорди Уильямсон из Сиднейского университета в лекции 2015 года.
Прошло более ста лет после её дебюта, и теория представлений стала ключевым ингредиентом во множестве важнейших математических открытий. Однако её ценность сложно оценить с первого раза.
«Не сразу становится понятно, что её стоит изучать», — сказала Эмили Нортон из Кайзерслаутернского технического университета в Германии.
Читать полностью »
Изучение нейтрино привело к неожиданному открытию в математике
2019-12-18 в 11:00, admin, рубрики: математика, матрицы, Научно-популярное, нейтринные осцилляции, нейтрино, собственные вектора, собственные числа, физикаТри физика хотели обсчитать процесс изменения нейтрино. В итоге они обнаружили неожиданное взаимоотношение между одними из самых распространённых объектов математики.
Однажды в августе, утром после завтрака математик Теренс Тао открыл емейл, написанный тремя физиками, с которыми он не был знаком. Троица объяснила ему, что наткнулась на простую формулу, которая в случае, если она окажется верной, опишет неожиданное взаимоотношение между одними из наиболее базовых и важных объектов линейной алгебры.
Формула «выглядела слишком хорошо, чтобы быть правдой», сказал Тао, профессор из Калифорнийского университета в Лос-Анджелесе, лауреат Филдсовской премии, один из ведущих математиков мира. «Нечто настолько короткое и простое уже давно должно было оказаться в учебниках, — сказал он. – Поэтому сначала я подумал – нет, этого не может быть».
А потом он подумал ещё немного.
Читать полностью »
Математика в Gamedev по-простому. Матрицы и аффинные преобразования
2018-12-09 в 12:55, admin, рубрики: .net, algorithms, C#, CGI (графика), Gamedev, gamedevelopment, math, matrix, unity, unity3d, геймдев, игры, математика, матрицы, разработка игр, юнитиВсем привет! Меня зовут Гриша, и я основатель CGDevs. Сегодня хочется продолжить тему математики в геймдеве. В предыдущей статье были показаны базовые примеры использования векторов и интегралов в Unity проектах, а сейчас поговорим о матрицах и аффинных преобразованиях. Если вы хорошо разбираетесь в матричной арифметике; знаете, что такое TRS и как с ним работать; что такое преобразование Хаусхолдера – то вы возможно не найдёте для себя ничего нового. Говорить мы будем в контексте 3D графики. Если же вам интересна эта тема – добро пожаловать под кат.
Доступно о кватернионах и их преимуществах
2018-10-19 в 5:12, admin, рубрики: кватернионы, математика, матрицы, поворот, Работа с 3D-графикой, углы Эйлера
От переводчика: ровно 175 лет и 3 дня назад были изобретены кватернионы. В честь этой круглой даты я решил подобрать материал, объясняющий эту концепцию понятным языком.
Концепция кватернионов была придумана ирландским математиком сэром Уильямом Роуэном Гамильтоном в понедельник 16 октября 1843 года в Дублине, Ирландия. Гамильтон со своей женой шёл в Ирландскую королевскую академию, и переходя через Королевский канал по мосту Брум Бридж, он сделал потрясающее открытие, которое сразу же нацарапал на камне моста.
Памятная табличка на мосту Брум Бридж через Королевский канал в честь открытия фундаментальной формулы умножения кватернионов.
В этой статье я постараюсь объяснить концепцию кватернионов простым для понимания образом. Я объясню, как можно визуализировать кватернион, а также расскажу о разных операциях, которые можно выполнять с кватернионами. Кроме того, я сравню использование матриц, углов Эйлера и кватернионов, а затем попытаюсь объяснить, когда стоит использовать кватернионы вместо углов Эйлера или матриц, а когда этого делать не нужно.
Читать полностью »