Перевод поста Майкла Тротта (Michael Trott), «Constructing Crossword Arrays Faster».
Скачать перевод в виде документа Mathematica, который содержит весь код использованный в статье, можно здесь.
В главе 6 моей книги Mathematica GuideBook for Programming, в качестве примера работы со списками я обсудил то, как построить массив, представляющий собой кроссворд. Хотя этот пример был хорош для демонстрации продвинутой работы со списками, тем не менее, использование списков не является оптимальным путем построения массива кроссворда. Сложность добавления нового слова в массив с уже размещенными n-1 словами составляла для этого алгоритма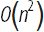 
, таким образом общая сложность составления массива кроссворда из n слов становилась равной 
.
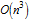На протяжении последних нескольких лет, некоторые пользователи Mathematica спрашивали меня о том, можно ли построить более быстрый алгоритм. Ответ — да, можно. Если мы будем применять методы хеширования, то мы сможем быстро и за одно и тоже время проверять, можно ли использовать некоторый элемент массива и, следовательно, мы сможем снизить общую сложность алгоритма с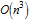 
до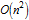 
, что для кроссвордов из тысяч слов даст большую разницу во времени, затрачиваемом на вычисления. Этот алгоритм реализован в данной статье. Когда мы размещаем отдельные буквы слова в некоторой прямоугольной таблице необходимо рассматривать множество различных ситуаций. В результате в статье содержится большее, чем обычно, количество процедурного кода. Хотя некоторые определения функций несколько длинные, благодаря комментариям между шагами вычислений и ветками решений код должен быть довольно простым для чтения и понимания.
Читать полностью »
