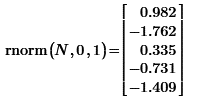На Хабре много статей посвящено алгоритмам Монте-Карло, например, вот эта, вчерашняя. Как основная идея, так и реализация методов весьма несложная, но небольшим препятствием может служить отсутствие под рукой подходящих инструментов для моделирования. Тем из читателей, для кого проблема актуальна, советую использовать бесплатный математический редактор Mathcad Express, про который я и пишу в моем блоге.
Mathcad Express — это «легкая» версия известного пакета PTC Mathcad Prime, в которой большая часть функционала выключена. Тем не менее, датчики псевдослучайных чисел остаются доступными, что позволяет реализовать (довольно быстро и наглядно) различные статистические модели на основе алгоритмов Монте-Карло. Сразу оговорюсь, что некоторые решения будут не самыми лучшими, с точки зрения пользователей коммерческой версии Mathcad Prime, однако, они гарантированно не выведут нас за пределы функционала бесплатного Mathcad Express.
Напомню, что алгоритмы Монте-Карло — это общее название группы численных методов, основанных на программном создании определенной последовательности псевдослучайных чисел, моделирующей тот или иной эффект, например, последовательность отказов техники. Получив большое число реализаций случайного процесса, можно надеяться, что его вероятностные характеристики совпадут с аналогичными величинами решаемой задачи «реального мира». Файл с дальнейшими расчетами в форматах Mathcad и XPS лежит здесь.
Часть 1. Как сгенерировать выборку псевдослучайных чисел
В Mathcad Express доступен ряд генераторов псевдослучайных чисел, создающих выборки псевдослучайных данных с различными законами распределения. Для создания вектора из N псевдослучайных чисел нужна всего лишь одна строка Mathcad-документа. Например сгенерировать N=5 псевдослучайных чисел с нормальным распределением (нулевым средним и единичной дисперсией) можно так:
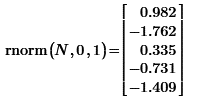
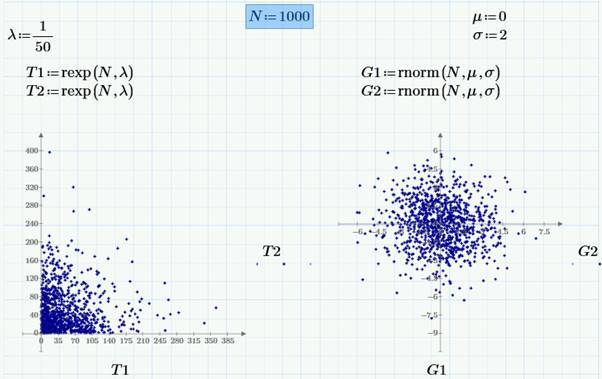
Векторы случайных чисел удобно визуализировать на графиках так: одна выборка (т.е. компоненты одного из случайных векторов T1) по оси абсцисс, а другая выборка (другой случайный вектор T2) – по оси ординат. На следующем рисунке приведены графики пар псевдослучайных чисел для экспоненциального (слева) и нормального (справа) распределения. Параметры распределений задаются в формулах над графиками.
Читать полностью »