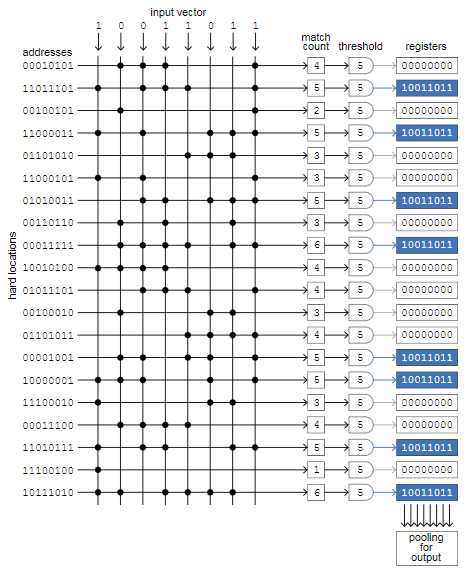
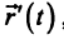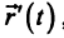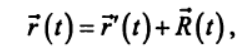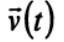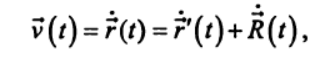Светлой памяти моего учителя — первого декана физико-математического факультета Новочеркасского политехнического института, заведующего кафедрой «Теоретическая механика» Кабелькова Александра Николаевича
Введение
Август, лето подходит к концу. Народ яростно рванул на моря, да оно и неудивительно — самый сезон. А на хабре, тем временем, буйным цветом распускается и пахнет лженаука. Если говорить о теме данного выпуска «Моделирования...», то в нем мы совместим приятное с полезным — продолжим обещанный цикл и совсем чуть-чуть поборемся с этой самой лженаукой за пытливые умы современной молодежи.

А вопрос ведь действительной не праздный — со школьных лет мы привыкли считать, что наш ближайший спутник в космическом пространстве — Луна движется вокруг Земли с периодом 29,5 суток, особенно не вдаваясь в сопутствующие подробности. На самом же деле наша соседка своеобразный и в какой-то степени уникальный астрономический объект, с движением которого вокруг Земли не всё так просто, как, возможно хотелось бы некоторым моим коллегам из ближайшего зарубежья.
Итак, оставив полемику в стороне, попытаемся с разных сторон, в меру своей компетенции, рассмотреть эту безусловно красивую, интересную и очень показательную задачу.