Что вы будете делать, если вас попросят решить простенькую систему с тремя неизвестными? У каждого сформировался свой собственный и наиболее удобный лично для него подход. Существует масса способов решить систему линейных алгебраических уравнений. Но почему предпочтение отдается именно методу Гаусса?
Читать полностью »
Рубрика «математика» - 82
Почему Гаусс? (100 способов решить систему уравннений)
2018-07-25 в 15:07, admin, рубрики: java, Алгоритмы, математика, системы линейных уравнений«Туда и обратно» для нейронных сетей, или обзор применений автокодировщиков в анализе текстов
2018-07-25 в 10:28, admin, рубрики: Алгоритмы, анализ данных, антиплагиат, Блог компании «Антиплагиат», математика, машинное обучение, обработка текста, Семантика, тематическое моделированиеМы уже писали в самой первой статье нашего корпоративного блога о том, как работает алгоритм обнаружения переводных заимствований. Лишь пара абзацев в той статье посвящена теме сравнения текстов, хотя идея достойна гораздо более развернутого описания. Однако, как известно, обо всем сразу рассказать нельзя, хоть и очень хочется. В попытках воздать должное этой теме и архитектуре сети под названием «автокодировщик», к которой мы питаем очень теплые чувства, мы с Oleg_Bakhteev и написали этот обзор.
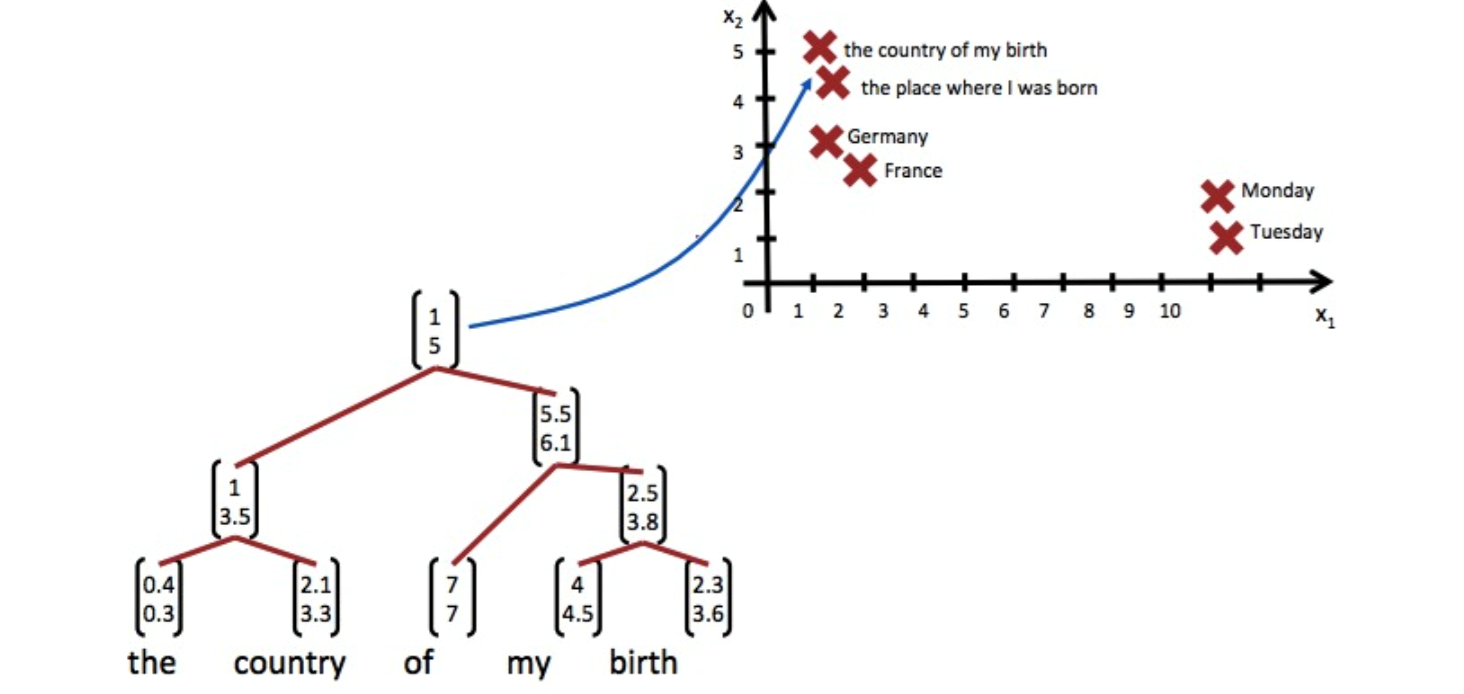
Источник: Deep Learning for NLP (without Magic)
Как мы упоминали в той статье, сравнение текстов у нас было “смысловое” – мы сопоставляли не сами текстовые фрагменты, а векторы, им соответствующие. Такие векторы получались в результате обучения нейронной сети, которая отображала текстовый фрагмент произвольной длины в вектор большой, но фиксированной размерности. Как получить такое отображение и как научить сеть выдавать нужные результаты – отдельный вопрос, о которой и пойдет речь ниже.
Читать полностью »
Объединение сортировки подсчётом и деревом
2018-07-24 в 19:29, admin, рубрики: Алгоритмы, математика, ПрограммированиеДоброго времени суток!
После телефонного собеседования в одну известную компанию, где меня попросили перечислить несколько видов сортировок (я назвал 10, к слову), я слегка озадачился этим вопросом.
Подумав минут 30 над этой проблемой, загуглив какие ещё есть виды сортировок, наткнулся на сортировку подсчётом. И пришёл к выводу, что её можно улучшить, что и постарался сделать.
Итак. Берём сортировку подсчётом и деревом.
Строим дерево Пар (Ключ, Количество), где Ключ отвечает за элемент массива, а Количество — количество повторений этого эл-та массива. Дерево, естественно, сбалансированное, АВЛ или чёрно-красное, но у АВЛ слишком жёсткие требования, так что второй вариант предпочтительнее.
Далее всё логично. Добавляем все элементы массива в Пару, а Пару ищем в дереве (чтобы избежать пересоздания объектов используем заранее созданную Пару, у которой меняем Ключ. Здесь Количество нас не интересует, поскольку мы ищем соответствие исключительно по Ключу). Если такой Ключ уже есть, увеличиваем Количество, иначе добавляем новую Пару (Ключ, 1).
Переписываем массив, удаляя каждый раз вершину и записывая Ключ столько раз, сколько у него Количество.
Читать полностью »
Использование функций JavaScript для построения 3D-моделей
2018-07-24 в 12:19, admin, рубрики: canvas, javascript, three.js, WebGL, математика, Работа с 3D-графикойВ данной статье рассмотрено применение геометрической библиотеки функций WebGeometry для построения моделей сложных многогранников. Библиотека написана на языке Javascript. Ссылка на GitHub с примером, в котором приведен простейший пример использования библиотеки. Замечания и критика приветствуются.
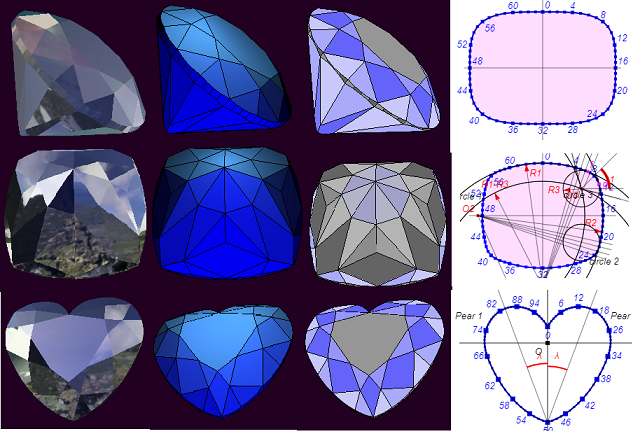
Для отображения моделей, предварительно рассчитанных с помощью функций из библиотеки WebGeometry, применяется библиотека ThreeJS. Холст (canvas) HTML5 используется для показа отдельных плоских элементов моделей и вывода на экран вспомогательной информации.
Читать полностью »
Бесконечный узор на основе простых чисел
2018-07-22 в 16:08, admin, рубрики: Алгоритмы, бесконечность, математика, ненормальное программирование, Программирование, простые числа, процедурная генерация, процедурная генерация карт, фракталы, фрактальные ландшафты
Привет! Однажды утром мне пришла в голову идея находить "исключающее ИЛИ" между координатами точки пространства и проверять полученное число на простоту. Результат такого простого алгоритма вы можете видеть на картинке. Подробнее под катом.
Читать полностью »
Компрессия больших массивов простых чисел
2018-07-21 в 7:30, admin, рубрики: C, компрессия данных, математика, простые числа, сжатие данных, теория чисел
Свойства простых чисел редко позволяют работать с ними иначе, чем в виде заранее вычисленного массива — и желательно как можно более объемного. Естественный формат хранения в виде целых чисел той или иной разрядности страдает при этом некоторыми недостатками, которые становятся существенными при росте объема данных.
Так, формат 16-разрядных беззнаковых целых при размере такой таблицы около 13 килобайт вмещает всего лишь 6542 простых числа: вслед за числом 65531 идут значения более высокой разрядности. Такая таблица годится разве что в качестве игрушки.
Наиболее ходовой в программировании формат 32-разрядных целых выглядит значительно солиднее — он позволяет хранить около 203 млн простых. Но такая таблица занимает уже около 775 мегабайт.
Еще больше перспектив у 64-разрядного формата. Однако при теоретической мощности порядка 1e+19 значений, таблица имела бы размер 64 экзабайта.
Теория счастья. Введение в мерфологию
2018-07-20 в 18:57, admin, рубрики: recreational science, занимательная математика, индекс Джини, кривая Лоренца, математика, Научно-популярное, парадокс инспекции, принцип Парето, теория вероятности и мат статистика, теория счастьяПродолжаю знакомить читателей Хабра с главами из своей книжки «Теория счастья» с подзаголовком «Математические основы законов подлости». Это ещё не изданная научно-популярная книжка, очень неформально рассказывающая о том, как математика позволяет с новой степенью осознанности взглянуть на мир и жизнь людей. Она для тех кому интересна наука и для тех, кому интересна жизнь. А поскольку жизнь наша сложна и, по большому счёту, непредсказуема, упор в книжке делается, в основном, на теорию вероятностей и математическую статистику. Здесь не доказываются теоремы и не даются основы науки, это ни в коем случае не учебник, а то, что называется recreational science. Но именно такой почти игровой подход позволяет развить интуицию, скрасить яркими примерами лекции для студентов и, наконец, объяснить нематематикам и нашим детям, что же такого интересного мы нашли в своей сухой науке.
Опубликованные главы:
Это, одна из первых глав, в которой на примере велосипедиста рассматриваются нужные нам инструменты для измерения несправедливости: кривая Лоренца и индекс Джини, а также упоминаются пресловутый Парето и грозный инспектор.

Что случилось с парадоксом Ферми
2018-07-15 в 11:30, admin, рубрики: астрономия, байесовская вероятность, земляне не читают теги, математика, Научно-популярное, парадокс ФермиПарадокс Ферми заключается в том, что вероятность возникновения внеземной цивилизации обычно оценивается довольно высоко, а признаков её существования что-то не видать. Недавно на arxiv появился препринт Сандерса с соавторами «Dissolving the Fermi paradox», который уже успели интерпретировать как отмену этого парадокса (правда), пустую болтовню в отсутствие данных (скорее правда, но верно для парадокса Ферми вообще, а не только для этой статьи), и как доказательство несуществования инопланетян и/или низкого L (неправда). В этой статье попробуем разобраться, что в препринте содержится на самом деле.

Теорема Бошерницана
2018-07-15 в 8:34, admin, рубрики: Блог компании Trinity Digital & Баласс Group, Занимательные задачки, изометрия, компакт, математика, метрическое пространство, расстояние, репетитор математика, теорема, теорема бошерницанаВ статье дано простое доказательство того, что отображение компактного метрического пространства в себя, не уменьшающее расстояния, является изометрией.
Отображение
 метрического пространства с метрикой
метрического пространства с метрикой  называют изометрией, если для любых
называют изометрией, если для любых  справедливо равенство
справедливо равенство  . Мы докажем здесь следующее утверждение:
. Мы докажем здесь следующее утверждение:
Теорема. Если
отображение компактного метрического пространства в себя, такое что
для любых
, то отображение
— изометрия.
Напомним некоторые простые утверждения о метрических компактах и введём некоторые соглашения и определения, необходимые для дальнейшего изложения.
Через 

Для 






Конечное множество 











Для любого конечного множества 




Читать полностью »
Капсульные нейронные сети
2018-07-15 в 7:23, admin, рубрики: big data, алгоритм динамической маршрутизации, Алгоритмы, искусственный интеллект, Капсульные сети, математика, машинное обучение, нейронные сетиВ 2017 году Джеффри Хинтон (один из основоположников подхода обратного распространения ошибки) опубликовал статью, в которой описал капсульные нейронные сети и предложил алгоритм динамической маршрутизации между капсулами для обучения предложенной архитектуры.
У классических свёрточных нейронных сетей есть недостатки. Внутреннее представление данных сверточной нейронной сети не учитывает пространственные иерархии между простыми и сложными объектами. Так, если на изображении в случайном порядке изображены глаза, нос и губы для свёрточной нейронной сети это явный признак наличия лица. А поворот объекта ухудшает качество распознавания, тогда, как человеческий мозг легко решает эту задачу.
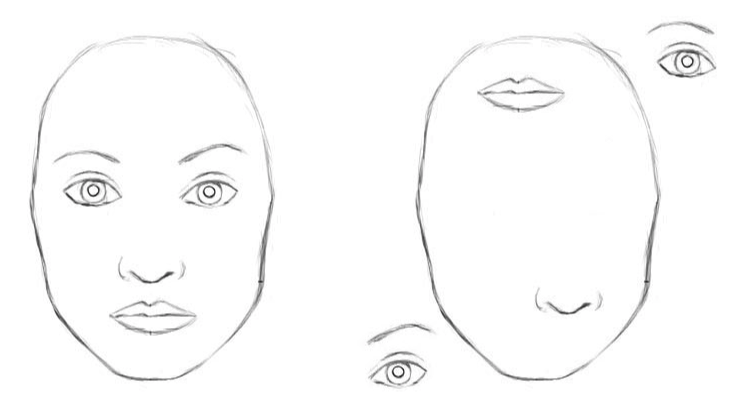
Для свёрточной нейронной сети 2 изображения схожи [2]
Читать полностью »

