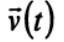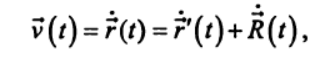
Системы отсчёта для определения орбиты
Для нахождения траекторий относительных движений в классической механике используется предположение об абсолютности времени во всех системах отсчета (как инерциальных, так и неинерциальных).
Используя данное предположение, рассмотрим движение одной и той же точки в двух различных системах отсчета К и К', из которых вторая движется относительно первой с произвольной скоростью 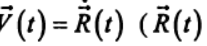 — радиус-вектор, описывающий положение точки начала системы координат К' относительно системы отсчета К).
— радиус-вектор, описывающий положение точки начала системы координат К' относительно системы отсчета К).
Будем описывать движение точки в системе К' радиус-вектором 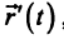 , направленным из начала координат системы К' в текущее положение точки. Тогда движение рассматриваемой точки относительно системы отсчета К описывается радиус-вектором
, направленным из начала координат системы К' в текущее положение точки. Тогда движение рассматриваемой точки относительно системы отсчета К описывается радиус-вектором 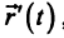 :
:
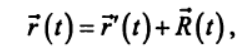 (1)
(1)
а относительная скорость