Попалась мне неплохая статья, про метод спектрального оценивания, который отлично подходит для короткого сигнала из суммы слабозашумленных гармоник. (-копия) Возможно, мои комментарии помогут читателю вникнуть в суть метода. Что немного огорчило, так это не до конца реализованные возможности метода. Метод применен для радиолокации — для быстрого определения направления на приходящие сигналы (угла θ) с последующей целью автоматической, надо понимать, адаптации системы. Но — численного определения этого угла автор не производит (причем по контексту это странно), хотя это определение вполне возможно. Имеем только красивые графики, по которым, получается, системе надо еще «ползать» и «ползать», определяя количество и расположение максимумов, что не совсем хорошо.
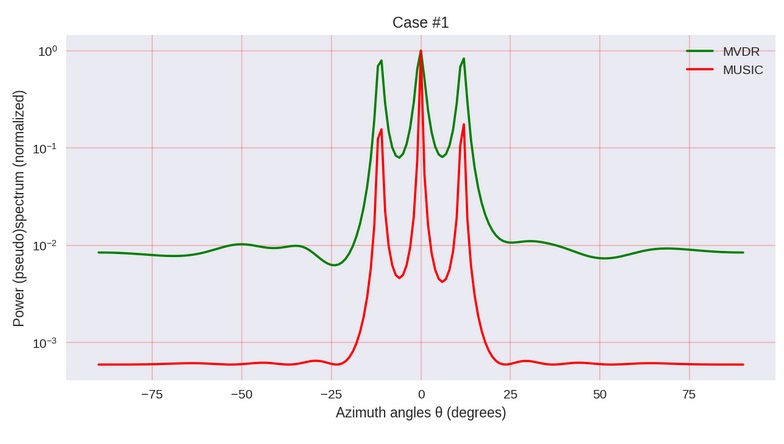
Иллюстрация автора упомянутой статьи
Читать полностью »
Рубрика «математика» - 53
О применении параметрических методов спектрального оценивания в радиолокации — метод MUSIC. Дополнение к статье
2019-06-09 в 10:45, admin, рубрики: data mining, EVD, MDVR, music, RootMUSIC, SVD, Алгоритмы, математика, спектральное оцениваниеКак устроен формат JPEG
2019-06-06 в 7:00, admin, рубрики: IT-стандарты, jpeg, jpg, Алгоритмы, графические файлы, жпг, математика, обработка изображений, сжатие данных, Форматы данныхИзображения формата JPEG встречаются повсюду в нашей цифровой жизни, но за этим покровом осведомлённости скрываются алгоритмы, устраняющие детали, не воспринимаемые человеческим глазом. В итоге получается высочайшее визуальное качество при наименьшем размере файла – но как конкретно всё это работает? Давайте посмотрим, чего именно не видят наши глаза!

Легко принять, как само собой разумеющееся, возможность отправить фотку другу, и не волноваться по поводу того, какое устройство, браузер или операционную систему он использует – однако так было не всегда. К началу 1980-х компьютеры умели хранить и показывать цифровые изображения, однако по поводу наилучшего способа для этого существовало множество конкурирующих идей. Нельзя было просто отправить изображение с одного компьютера на другой и надеяться, что всё заработает.
Читать полностью »
Город без пробок
2019-06-04 в 11:21, admin, рубрики: smart city, Алгоритмы, математика, математика и реальная жизнь, транспорт, транспорт будущего, Урбанизм
Глава первая.
Искусство разумно применять светофоры
Маленькое предисловие
Каждый день, оказываясь рядом с перекрестком, мы наблюдаем одну и ту же картину, как на зеленый свет машины мчатся вперед, а на красный — они скапливаются перед светофором в длинные очереди бесполезного ожидания. Но насколько привычное является одновременно необходимым и можно ли сделать так, чтобы в своем путешествии по городу автомобилистам почти не приходилось «стоять» на красный свет? Я думаю, многие из нас слышал о мифических «зеленых волнах». Попав в такую волну и поддерживая определенную скорость, автомобилист чудесным образом будет подъезжать к каждому перекрестку как раз в то время, когда светофор горит в его сторону зеленым светом. Довольно просто организовать распространение таких «волн» вдоль одной изолированной дороги, но совсем не очевидно, можно ли это сделать на дорогах всего города сразу.
Читать полностью »
Вопросы приоритета: Найквист, Шеннон или Котельников?
2019-06-02 в 13:41, admin, рубрики: Алгоритмы, Исследования и прогнозы в IT, Котельников В.А., математика, Найквист, наука, приоритет, Профессиональная литература, теорема выборок, теорема отсчётов, Читальный зал, ШеннонО приоритете работ в области передачи информации.
Первопроходцем в этом современном вопросе является В.А.Котельников. Во время аспирантуры в МЭИ были опубликованы в 1932г. работы, одна из которых называлась «О пропускной способности „эфира“ и проволоки в электросвязи» и заявлена к докладу I Всесоюзного съезда по вопросам технической реконструкции дела связи и развития слаботочной промышленности. Съезд не состоялся. Была опубликована в 1933г. как материал к докладу (принят к печати в
ноябре 1932г.). Читать полностью »
Жизнь на частицах 3D
2019-06-01 в 17:55, admin, рубрики: CUDA, game of life, ogre3d, Алгоритмы, игра жизнь, клеточные автоматы, математика, параллельное программирование, Программирование, разработка игр, частицыПривеТ! Решил поделиться с читателями своими небольшими экспериментами с системами частиц в трехмерном пространстве. За основу взял публикацию на Хабре об экспериментах с частицами в 2D пространстве.

Ричард Хэмминг: Глава 13. Теория информации
2019-06-01 в 16:25, admin, рубрики: CAI, Learning to Learn, Алгоритмы, будущее, Исследования и прогнозы в IT, математика, Профессиональная литература, ричард хэмминг, Системная инженерия, форсайт, цифровая экономика, Читальный залМы это сделали!
«Цель этого курса — подготовить вас к вашему техническому будущему.»
 Привет. Помните офигенную статью «Вы и ваша работа» (+219, 2588 в закладки, 429k прочтений)?
Привет. Помните офигенную статью «Вы и ваша работа» (+219, 2588 в закладки, 429k прочтений)?
Так вот у Хэмминга (да, да, самоконтролирующиеся и самокорректирующиеся коды Хэмминга) есть целая книга, написанная по мотивам его лекций. Мы ее переводим, ведь мужик дело говорит.
Это книга не просто про ИТ, это книга про стиль мышления невероятно крутых людей. «Это не просто заряд положительного мышления; в ней описаны условия, которые увеличивают шансы сделать великую работу.»
За перевод спасибо Андрею Пахомову.
Теория Информации была разработана К. Э. Шенноном в конце 1940х годов. Руководство Лабораторий Белла настаивало, чтобы он назвал ее «Теория Связи», т.к. это намного более точное название. По очевидным причинам, название «Теория Информации» обладает значительно большим воздействием на публику, поэтому Шеннон выбрал именно его, и именно оно известно нам по сей день. Само название предполагает, что теория имеет дело с информацией, это и делает ее важной, поскольку мы все глубже проникаем в информационную эпоху. В этой главе я затрону несколько основных выводов из этой теории, приведу не строгие, а скорее интуитивно понятные доказательства некоторых отдельных положений этой теории, чтобы вы поняли, чем на самом деле является «Теория Информации», где вы можете ее применять, а где нет.
Читать полностью »
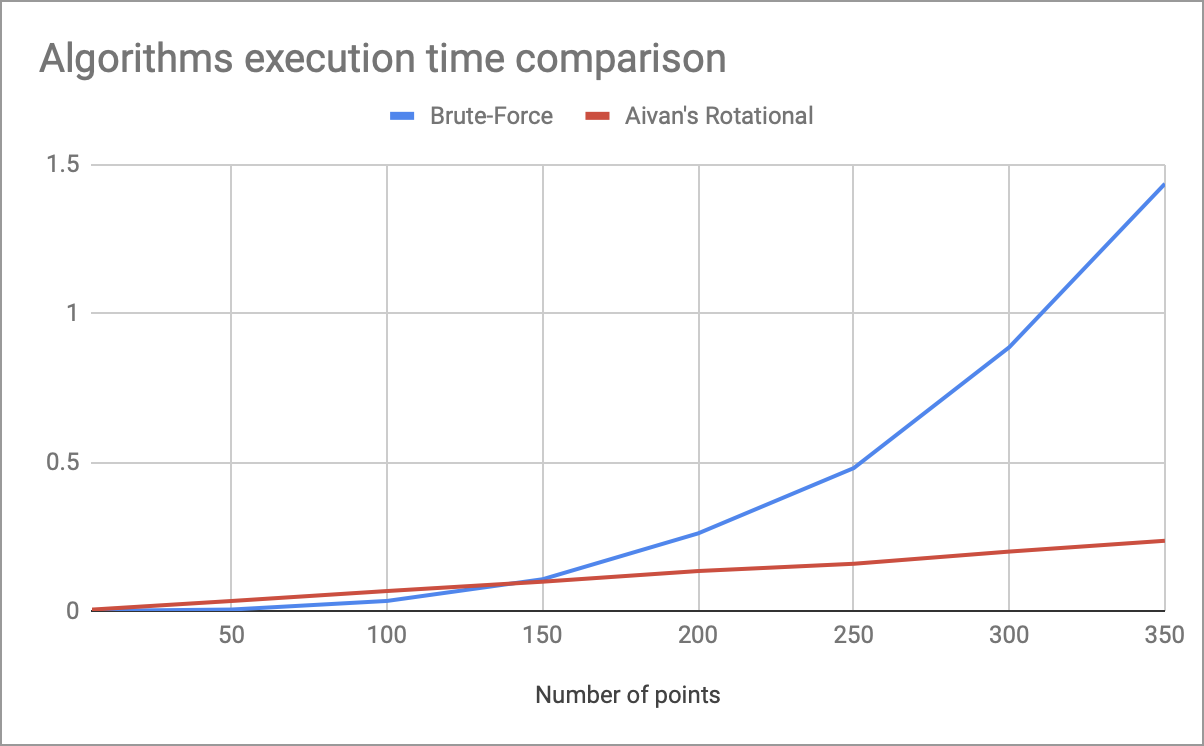
ARA: алгоритм для нахождения максимального числа точек на прямой линии
2019-06-01 в 0:49, admin, рубрики: complexity, python, алгоритм, Алгоритмы, математика, собеседованиеНедавно мне попалась классическая задачка для собеседований: поиск максимального числа точек, стоящих на прямой линии (на плоскости, координаты целочисленные). В голову сразу пришла идея полного перебора, которая имеет очевидную сложность по времени в O(n^2), но мне показалось, что здесь обязано быть что-то ещё, хоть какая-то альтернатива в O(n*log(n)). Через полчаса нашлось даже нечто лучшее!
Математические неопределенности на примере Python
2019-05-31 в 15:18, admin, рубрики: iee754, javascript, python, математика, числаВсем привет! Мы очень часто пользуемся привычными числами в наших любимых языках программирования. Привычные это 1, -1.5, pi или даже комплексные. А вот NaN, +Inf, -Inf используется нами гораздо реже.
Примечание:
В статье я использую элементарные функции Python версии 3.6.8, но многое будет актуально и для других языков, например для JS.
Читать полностью »
Как устроено A-B-тестирование в Авито
2019-05-31 в 8:56, admin, рубрики: АБ-тесты, аналитика, Аналитика мобильных приложений, веб-аналитика, визуализация данных, математика, метрикиВсем привет. Меня зовут Данила, я работаю в команде, которая развивает аналитическую инфраструктуру в Авито. Центральное место в этой инфраструктуре занимает А/B-тестирование.
А/B эксперименты — ключевой инструмент принятия решений в Авито. В нашем цикле продуктовой разработки А/B-тест является обязательным этапом. Мы проверяем каждую гипотезу и выкатываем только позитивные изменения.
Мы собираем сотни метрик и умеем детализировать их до бизнес-разрезов: вертикали, регионы, авторизованные пользователи и т. д. Мы делаем это автоматизированно с помощью единой платформы для экспериментов. В статье я достаточно подробно расскажу, как платформа устроена и мы с вами погрузимся в некоторые интересные технические детали.

Самая красивая теорема математики: тождество Эйлера
2019-05-31 в 7:20, admin, рубрики: кватернионы, комплексные числа, математика, Научно-популярное, тождество эйлера, тригонометрия, число пиПосмотрев лекцию профессора Робина Уилсона о тождестве Эйлера, я наконец смог понять, почему тождество Эйлера является самым красивым уравнением. Чтобы поделиться моим восхищением это темой и укрепить собственные знания, я изложу заметки, сделанные во время лекции. А здесь вы можете купить его прекрасную книгу.
Что может быть более загадочным, чем взаимодействие мнимых чисел с вещественными, в результате дающее ничто? Такой вопрос задал читатель журнала Physics World в 2004 году, чтобы подчеркнуть красоту уравнения Эйлера «e в степени i, умноженного на пи равно минус единице».
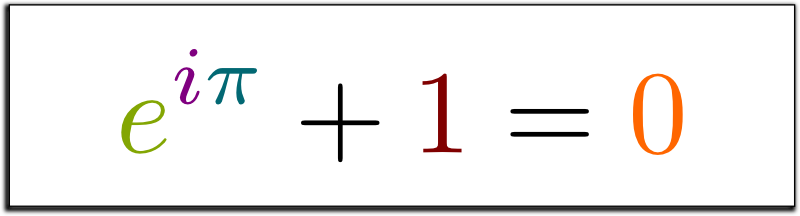
Рисунок 1.0: тождество Эйлера — e в степени i, умноженного на пи, плюс единица равно нулю.
Ещё раньше, в 1988 году, математик Дэвид Уэллс, писавший статьи для американского математического журнала The Mathematical Intelligencer, составил список из 24 теорем математики и провёл опрос, попросив читателей своей статьи выбрать самую красивую теорему. И после того, как с большим отрывом в нём выиграло уравнение Эйлера, оно получило званием «самого красивого уравнения в математике».
Читать полностью »