Хотели посмотреть на мир глазами существа живущего в компактной замкнутой вселенной со сферической геометрией? Посмотреть на мир без ночи? Мир, где на небе виден другой полюс планеты? Мир, где нет разницы между солнечным и лунным затмением? Добро пожаловать под кат!
Рубрика «математика» - 51
Мир трехмерной гиперсферы. Геодезическая трассировка лучей в замкнутой вселенной со сферической геометрией
2019-07-29 в 3:38, admin, рубрики: javascript, WebGL, астрономия, геометрия Вселенной, гиперсфера, замкнутая вселенная, математика, Научно-популярное, сферическая геометрия, трассировка лучейВот зачем нужна школьная алгебра
2019-07-28 в 12:10, admin, рубрики: математика, математика и программирование, математика и реальная жизнь, Учебный процесс в IT, школьное образованиеОбычно на вопрос «зачем нужна математика?» отвечают что-то вроде «гимнастика для ума». На мой взгляд, этого объяснения недостаточно. Когда человек выполняет физические упражнения, то он знает точное название групп мышц, которые при этом развиваются. Но разговоры про математику остаются слишком абстрактными. Какие конкретно «мышцы ума» тренируются школьной алгеброй? Она ведь совсем не похожа на настоящую математику, в которой делаются великие открытия. Что дает умение искать производную каких-то запутанных функций?
Преподавание программирования слабым студентам привело меня к более точному ответу на вопрос «зачем?». В статье я постараюсь донести его вам.

Почему доказательство Великой теоремы Ферма не нуждается в улучшениях
2019-07-26 в 7:00, admin, рубрики: великая теорема ферма, информатика, логика, математика, Научно-популярное, научный метод, теория чиселВ течение десятилетий, прошедших после появления знакового доказательства великой теоремы Ферма, появилось несколько идей по поводу того, как сделать его ещё более надёжным. Однако эти попытки отражают глубокое непонимание того, что делает доказательство важным.

23 июня исполнилось 25 лет с момента взбудоражившего всех объявления от Эндрю Уайлса, в котором он заявил о получении доказательства великой теоремы Ферма – наиболее известной в математике задачи возрастом 350 лет. История, окружающая доказательство Уайлса – семь лет он тайно работал над этим проектом, разрыв в доказательстве, обнаружившийся после июньского объявления, элегантное решение, опубликованное год спустя в совместной работе, написанной Уайлсом вместе с его бывшим студентом Ричардом Тэйлором, получение рыцарского звания в 2000 – вошло в анналы математических легенд.
Читать полностью »
Жадный подход и игровые автоматы. Разбор задач ML-трека чемпионата по программированию
2019-07-25 в 7:51, admin, рубрики: Блог компании Яндекс, Занимательные задачки, конкурсы, конкурсы разработчиков, математика, машинное обучение, многорукие бандиты, рекомендательные системы, Спортивное программирование, Яндекс.Блиц
Мы продолжаем публиковать разборы задач, которые предлагались на недавнем чемпионате. На очереди — задачи, взятые из квалификационного раунда для специалистов по машинному обучению. Это третий трек из четырёх (бэкенд, фронтенд, ML, аналитика). Участникам нужно было сделать модель исправления опечаток в текстах, предложить стратегию игры на игровых автоматах, довести до ума систему рекомендаций контента и составить ещё несколько программ.
Равномерное распределение точек на сфере
2019-07-22 в 5:56, admin, рубрики: Алгоритмы, аппроксимация, додекаэдр, золотое сечение, икосаэдр, математика, Работа с 3D-графикой, распределение точек, сфера, фибоначчиКак можно более равномерное распределение точек на сфере — невероятно важная задача в математике, науке и компьютерных системах, а наложение сетки Фибоначчи на поверхность сферы при помощи равновеликой проекции — чрезвычайно быстрый и эффективный метод аппроксимации для её решения. Я покажу, как благодаря незначительным изменениям его можно сделать ещё лучше.

Какое-то время назад этот пост появился на главной странице Hacker News. Его обсуждение можно прочитать здесь.
Введение
Задача равномерного распределения точек на сфере имеет очень долгую историю. Это одна из самых хорошо исследованных задач в математической литературе по сферической геометрии. Она имеет критическую важность во многих областях математики, физики, химии, в том числе в вычислительных методах, теории приближений, теории кодирования, кристаллографии, электростатике, компьютерной графике, морфологии вирусов и многих других.
К сожалению, за исключением нескольких особых случаев (а именно платоновых тел) невозможно идеально ровно распределить точки на сфере. Кроме того, решение задачи сильно зависит от критерия, который используется для оценки однородности. На практике используется множество критериев, в том числе:
- Упаковка и покрытие
- Выпуклые оболочки, ячейки Вороного и треугольники Делоне
- Ядра
-энергии Риса
- Кубатура и определители
Очень важно уяснить этот аспект: обычно не существует единственного оптимального решения этой задачи, потому что оптимальное решение, основанное на одном критерии, часто не является оптимальным распределением точек для других. Например, мы также выясним, что оптимизация упаковки необязательно создаёт оптимальную выпуклую оболочку и наоборот.
Ради краткости в этом посте мы рассмотрим только два критерия: минимальное расстояние упаковки и выпуклую оболочку/сетку Делоне (объём и площадь).
Читать полностью »
Модельно ориентированное проектирование. Электропривод с бесколлекторным двигателем постоянного тока
2019-07-22 в 5:14, admin, рубрики: Matlab, SimInTech, Simulink, автоматическое управление, Алгоритмы, Анализ и проектирование систем, генерация кода, математика, математическое моделирование, проектирование, Промышленное программирование, электроприводыВ предыдущей статье про модельно ориентированное проектирование было показано, что не все методики одинаково полезны. И объясняется как делать правильно, что бы не было потом мучительно больно. Но в конце статье был поставлен вопрос, провокационный как Шарон Стоун на допросе у следователей:
Модельно ориентированное проектирование это конечно хорошо, но как доказать, что модель соответствует объекту? Какие ваши доказательства?

Общий ответ на данный вопрос еще готовится, но про частный зато реальный и свежий пример могу привести прямо сейчас. Оказался тут у меня в руках, как всегда случайно, текст от ведущего специалиста нашей страны по электроприводу Калачева Юрия Николаевича, вместе с его любезным согласием на публикацию. Данный текст еще готовится к публикации в специализированных издания, но читатели хабра увидят его первые.
Далее под катом
Калачев Ю. Н., Ланцев В.Ю., Окулов Е.В.
Электропривод с бесколлекторным двигателем постоянного тока
(практика применения моделирования и кодогенерации в АО «Аэроэлектромаш»)
Читать полностью »
Физик рассчитал, что жизнь всё-таки возможна в 2D-вселенной
2019-07-19 в 13:29, admin, рубрики: антропный принцип, астрономия, голографический принцип, гравитация, двумерная вселенная, математика, Научно-популярное, планарные графы, физика
Окружающая реальность существует в трёхмерной Вселенной (плюс время), поэтому нам трудно представить Вселенную только с двумя измерениями. Согласно антропному принципу, мы видим Вселенную такой, потому что только в такой Вселенной мог возникнуть наблюдатель, человек. Другими словами, мы наблюдаем заведомо не произвольную область Вселенной, а ту, особая структура которой сделала её пригодной для возникновения и развития жизни.
Соответственно, во Вселенной встречаются разные значения мировых констант, но мы не можем их наблюдать. Впрочем, по расчётам физика Джеймса Скарджилла (James Scargill) из Калифорнийского университета в Дэвисе, двумерная Вселенная всё-таки возможна.
В частности, Скарджилл рассматривает идею жизни в измерениях 2+1, где +1 —это измерение времени.
Читать полностью »
Специалисты по информатике расширяют рубежи проверяемого знания
2019-07-18 в 7:00, admin, рубрики: IP, mip, neexp, np, графы, квантовая физика, квантовые компьютеры, квантовые технологии, математикаВселенная задач, проверяемых компьютером, выросла. Благодаря какому секретному ингредиенту это произошло? Из-за квантовой запутанности.

Представьте, что некто пришёл к вам и заявил, что у него есть оракул, способный раскрыть сокровенные тайны вселенной. Вы могли бы заинтересоваться этим, но вам тяжело было бы в это поверить. Вы бы хотели придумать способ подтвердить, что оракул говорит правду.
Такова основная проблема информатики. Некоторые задачи слишком сложно решить за разумное время. Но их решения просто проверить. Учитывая это, специалистам по информатике хочется знать: насколько сложной может быть задача, решение которой всё ещё можно проверить?
Оказывается, что ответ на этот вопрос: практически невообразимо сложной.
Читать полностью »
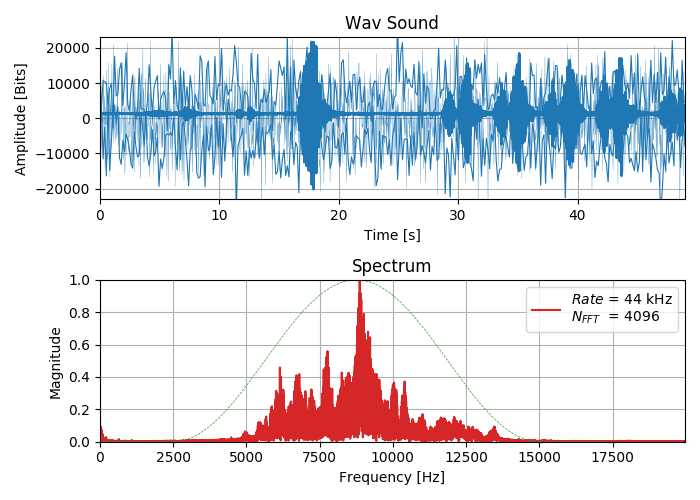
Курс лекций «Основы цифровой обработки сигналов»
2019-07-18 в 5:15, admin, рубрики: digital-signal-processing, dsp, Matlab, matplotlib, numpy, open source, python, python3, scipy, Алгоритмы, быстрое преобразование фурье, математика, цифровая обработка сигналов, цифровая фильтрацияВсем привет!
Часто ко мне обращаются люди с вопросами по задачам из области цифровой обработки сигналов (ЦОС). Я подробно рассказываю нюансы, подсказываю нужные источники информации. Но всем слушателям, как показало время, не хватает практических задач и примеров в процессе познания этой области. В связи с этим я решил написать краткий интерактивный курс по цифровой обработке сигналов и выложить его в открытый доступ.
Большая часть обучающего материала для наглядного и интерактивного представления реализована с использованием Jupyter Notebook. Предполагается, что читатель имеет базовые знания из области высшей математики, а также немного владеет языком программирования Python.
Белый шум рисует черный квадрат
2019-07-17 в 23:43, admin, рубрики: big data, data analysis, data mining, machine learning, Алгоритмы, анализ данных, декомпозиция баз данных, математика, открытые данные, теорема Эрдёша-РеньиЛюбой аналитик, в начале своей работы, проходит ненавистный этап определения идентификации параметров распределения. Потом, с наработкой опыта, для него согласование полученных остаточных разбросов означает, что какой-то этап, в анализе Big Data, пройден и можно двигаться дальше. Уже нет необходимости проверять сотни моделей на соответствие различным уравнениям регрессии, искать отрезки с переходными процессами, составлять композицию моделей. Терзать себя сомнениями: «Может есть, еще какая-нибудь модель, которая больше подходит?»
Подумал: «А что, если пойти от противного. Посмотреть, что может сделать белый шум. Может ли белый шум создать, что-то, что наше внимание сопоставит со значимым объектом из нашего опыта?»

Рис. Белый шум (файл взят из сети, размер 448х235).
По этому вопросу рассуждал так:
1. Какова вероятность, что появится горизонтальные и вертикальные линии, заметной длины?
2. Если они могут появиться, то какова вероятность, что они совпадут своим началом по одной из координат и составят прямоугольную фигуру?
Дальше по тексту, объясню, как эти задачи связались с анализом Big Data.
Читать полностью »