Приветствую всех! В прошлой части мы с вами получили уравнения движения системы из двух материальных точек, а также некоторую мотивацию на использование этой модели. Теперь же попробуем выжать как можно больше информации из них. Вот они:
begin{equation*}
begin{cases}
m_{1}ddot{vec{r}}_{1} = vec{F}_{12}, (1)
\
m_{2}ddot{vec{r}}_{2} = -vec{F}_{12},
end{cases}
end{equation*}
где
«Единственный смысл существование экономики — это воодушевление математиков на новые подвиги.»
В 2013 году Алексей Савватеев прочитал несколько лекций по моделям соцсетей и интернета. Я нашел эту тему очень любопытной и незаслуженно забытой. Попробуем разобраться в вопросе. А ещё мне интересно узнать, как изменилась ситуация с тех пор и какие полезные публикации есть в этой области.
И в интернете, и в биологии соцсети проявляют свойства, которые по отдельности описываются моделями, но все вместе — ставят в тупик современную математику. Савватеев утверждает утверждаю, что тот, кто с этим разберется получит Нобелевскую премию. Будущее будет зависеть от способности работать с сетями.
Ниже приводится скомпилированная выжимка из трёх видеозаписей лекций, само видео есть в конце. (Пост выглядит как набор слайдов с цитатами лектора, связать всё в единый и прилизанный текст у меня не хватает способностей к русскому языку и математике, но тема очень важная, поэтому хочу опубликовать.)
Читать полностью »
Одна из наиболее актуальных задач цифровой обработки сигналов – задача очистки сигнала от шума. Любой практический сигнал содержит не только полезную информацию, но и следы некоторых посторонних воздействий помехи или шума. Кроме этого, при вибродиагностике сигналы от вибродатчиков имеют не стационарный частотный спектр, что усложняет задачу фильтрации.
Существует множество различных способов удаления высокочастотного шума из сигнала. Например, библиотека Scipy содержит фильтры, основанные на различных методах фильтрации: Калмана; сглаживание сигнала путём его усреднения по оси времени, и другие.
Однако, преимущество метода дискретного вейвлет преобразования (DWT) состоит в многообразии форм вейвлет. Можно выбрать вейвлет, который будет иметь форму, характерную для ожидаемых явлений. Например, можно выделить сигнал в заданном частотном диапазоне, форма которого отвечает за появление дефекта.
Целью настоящей публикации является анализ методов фильтрации сигналов вибродатчиков с применением DWT преобразования сигнала, фильтра Калмана и метода скользящего среднего.
В публикации работу фильтров основанных на различных методах фильтрации будем анализировать используя набор данных НАСА. Данные получены на экспериментальной платформе PRONOSTIA:
Набор содержит данные о сигналах вибродатчиков по износу подшипников различных типов. Назначение папок с файлами сигналов приведено в таблице:
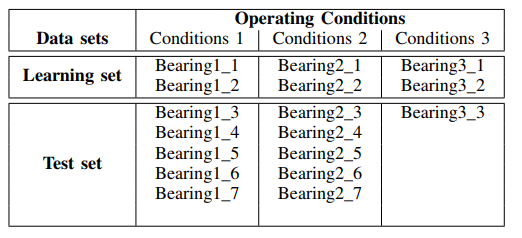
Мониторинг состояния подшипников обеспечивается сигналами датчиков вибрации (горизонтальным и вертикальным акселерометрами), силы и температуры.
Сигналы получены для трёх различных нагрузок:
Номинация: За проработку теории контрактов в неоклассической экономике. Неоклассическое направление подразумевает рациональность экономических агентов, широко использует теорию экономического равновесия и теорию игр.
Оливер Харт и Бенгт Хольмстрём.
Контракт. Что это такое? Я работодатель, у меня несколько сотрудников, я говорю им как будет устроена их зарплата. В каких случаях и что они будут получать. Эти случаи могут включать и поведение их коллег.
Приведу пять примеров. Три из них иллюстрируют, как попытка вмешательства привела к ухудшению ситуации.
Читать полностью »
В первой публикации рассказывалось о том, что есть подзабытая теорема Эрдёша-Реньи, из которой следует, что в случайном ряде, длины N, с вероятностью близкой к 1 существует подряд из одинаковых значений длиной log_2{N}. Указанное свойство случайной величины можно использовать для ответа на вопрос: «После обработки больших данных, подчиняется ли остаточный ряд закону случайных чисел или нет?»
Ответ на такой вопрос определялся не на основании тестов соответствия нормальности распределения, а на основании свойств самого остаточного ряда.
Читать полностью »
Разработана память с нелинейной аппроксимацией внутри кластеров данных. Кластеры предлагается выделять методом k-средних. Аппроксимацию проводить с помощью обучения ансамбля нейронных сетей. Кластерная память протестирована на примере адаптивного фильтра для преобразования цветов изображения. По результатам компьютерных экспериментов данный вид памяти показал хорошую селективную способность к обучению. На примере адаптивного фильтра удается обучить память к изменению всей цветовой палитры изображения.
Читать полностью »
Привет всем! Сегодня я начну серию статей-лекций посвященных теме проектирования беспилотных летательных аппаратов космического назначения (ракет) =). Да-да, — вы не ослышались, самых настоящих ракет, будем их учиться проектировать по настоящему, как это (наверное) делают в каком нибудь КБ . Сам я заканчивал универ именно по этой специальности, потому некоторые знания имеются. Но сам еще ни дня в КБ (к сожалению) не проработал. По причине соответственного расположения звезд на небосводе. В общем звезды так сошлись, судьба такая у меня. Хотя мог бы уже пол года работать в КБ Южном, зимой почти устроился, осталось лишь медкомиссию пройти и сдать документы на проверку в СБУ для получения допуска секретности. Но пошло опять что то не так. До этого уже шло очень много раз, потому наверное что то накопленное выстрелило, и я решил: в пе*ду да ну его.
А, кстати, месяц назад послал резюме в SpaceX на mechanical engineer, но мне через два дня вежливо отказали, потому что закон ITAR. Ну попытка не пытка, а я действительно просто хотел поехать чем нибудь помочь, и никакой я не спецагент. Ну да ладно, начну пожалуй по теме, а то развел тут историю своей жизни излагать. (просто чем то нужно было заполнить начало, думал-думал — написал как есть).
Читать полностью »
Скорее всего, вам известны следующие соотношения еще со школы:
Когда вы в детстве впервые познакомились с этой формулой, скорее всего, вашим первым чувством была боль из-за того, что эту формулу надо запомнить. Это очень плохо, потому что на самом деле вам не нужно запоминать эту формулу — она сама выводится, когда вы поворачиваете треугольник на бумаге. На самом деле, я делаю то же самое, когда записываю эту формулу. Это толкование будет очевидным к середине этой статьи. Но сейчас, чтобы оставить все веселье на потом и отодвинуть момент, когда вы скажете "Эврика!", давайте подумаем, а зачем нам вообще задумываться об этой формуле.
В 1985 году Институт инженеров электротехники и электроники (IEEE) установил стандарт IEEE 754, отвечающий за форматы чисел с плавающей запятой и арифметики, которому суждено будет стать образцом для всего железа и ПО на следующие 30 лет.
И хотя большинство программистов использует плавающую точку в любой момент без разбора, когда им нужно проводить математические операции с вещественными числами, из-за определённых ограничений представления этих чисел, быстродействие и точность таких операций часто оставляют желать лучшего.
Читать полностью »
