(с)
Среди ученых ходит байка о нетривиальном способе сделать свой доклад интересным и увлекательным. Во время выступления нужно выбрать в зале самого недоумевающего, самого потерянного слушателя, и рассказывать персонально ему, да так, чтобы зажечь в глазах огонек интереса.
Еще известен афоризм, приписываемый физику Ричарду Фейнману: «Если вы ученый, квантовый физик, и не можете в двух словах объяснить пятилетнему ребенку, чем вы занимаетесь, — вы шарлатан».
Доступно объяснять устройство сложных вещей — великий навык, однако бывают истории, о которые сломает язык даже самый искусный оратор. Теория динамических систем – вот та область, где без визуализации чувствуешь себя слепым садовником в окружении колючих, увенчанных шипами растений.
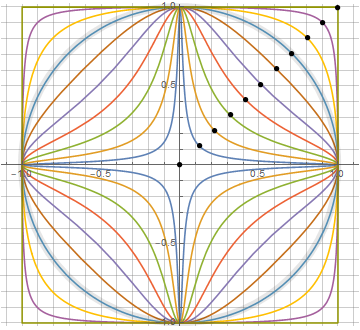
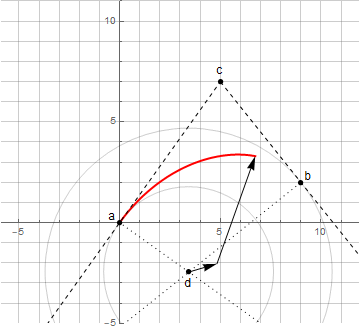
Сложные непериодические режимы поведения динамических систем можно описать непериодическими траекториями — так называемыми странными аттракторами, имеющими фрактальную структуру. Сегодня покажем, как визуализируют поведение странных и некоторых других аттракторов.
Читать полностью »