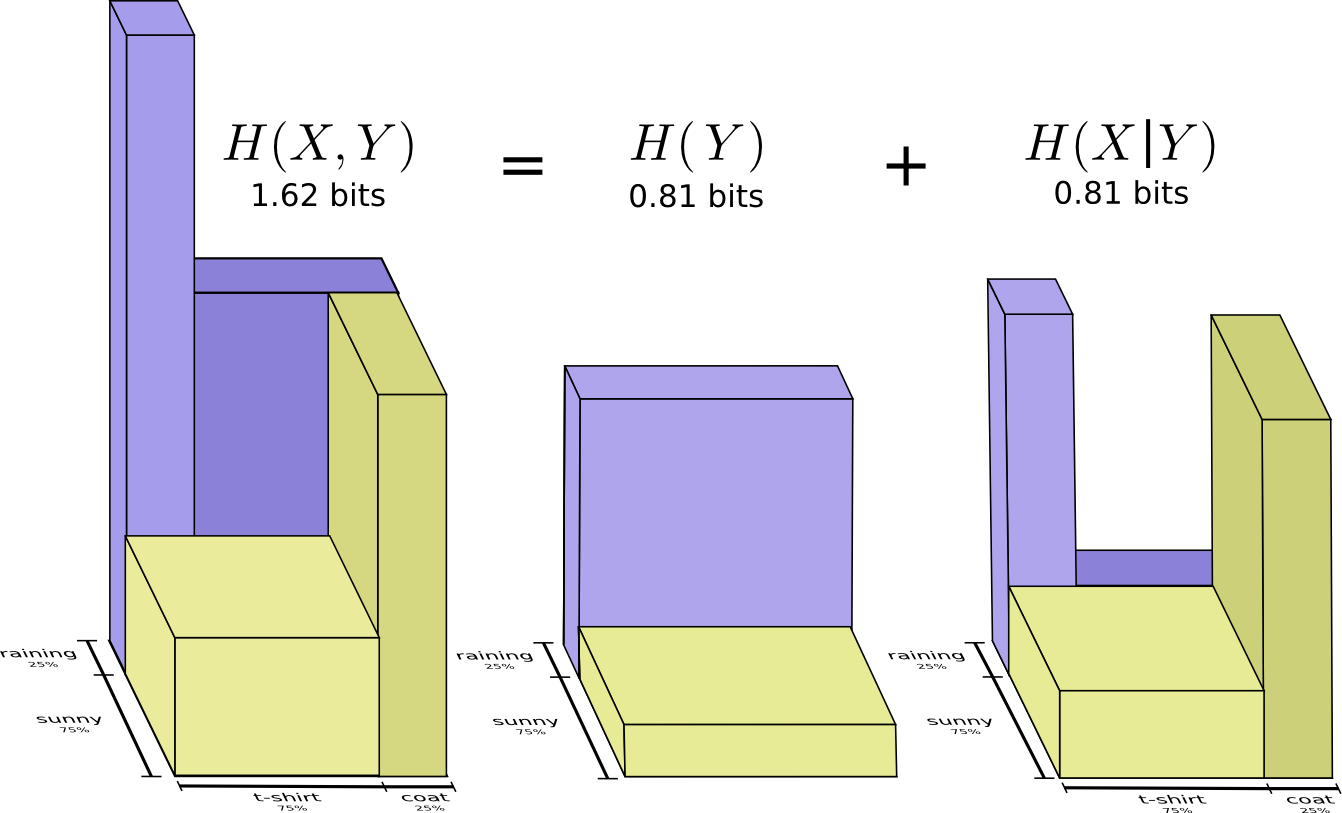
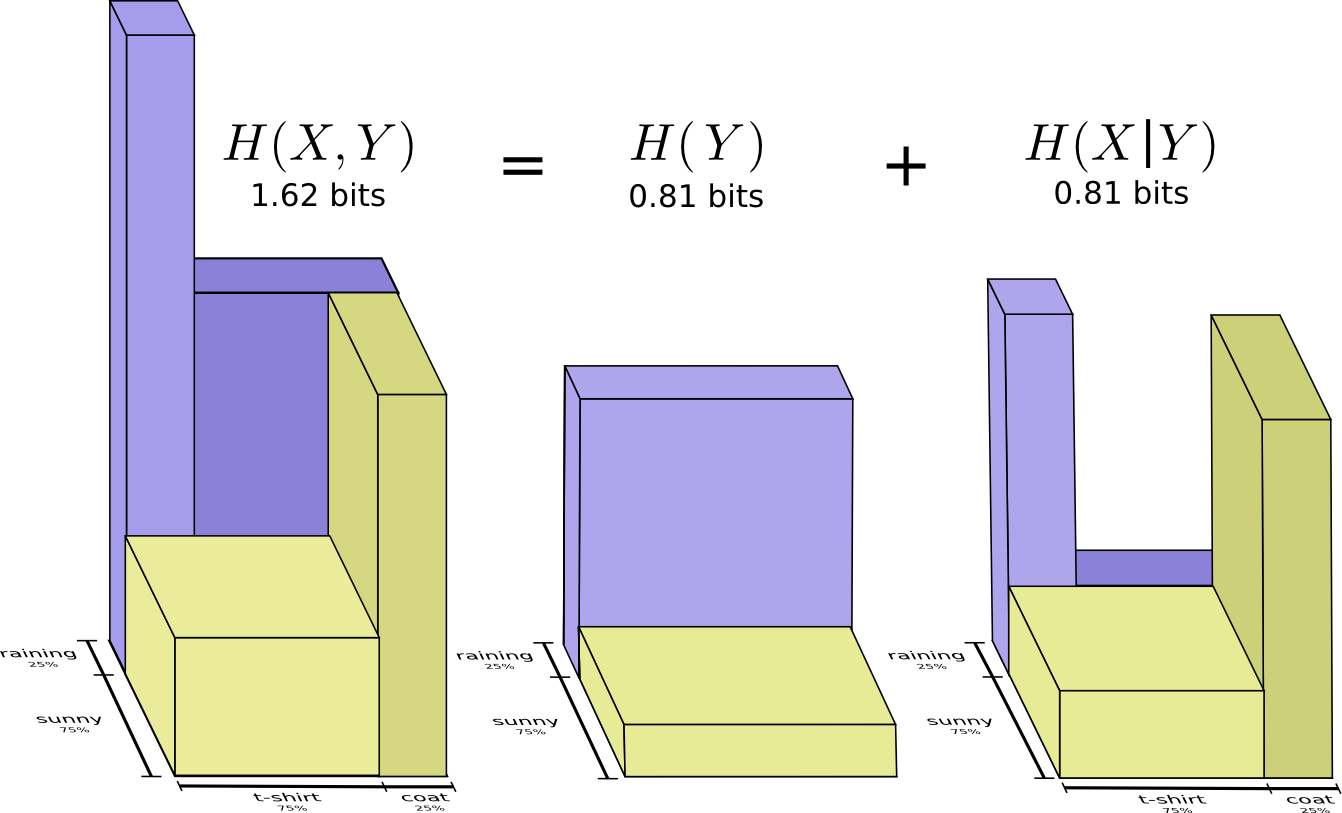
(Кто уже читал предыдущие части перевода этой лекции, перематывайте до таймкода 20:10)
[Хэмминг местами говорит очень неразборчиво, поэтому если есть пожелание по улучшению перевода отдельных фрагментов — пишите в личку.]
Этой лекции не было в расписании, но ее пришлось добавить, чтобы не возникало окна между занятиями. Лекция, в сущности, посвящена тому, как мы знаем то, что мы знаем, если, конечно, мы и в самом деле это знаем. Эта тема стара как мир – она обсуждается последние 4000 лет, если не дольше. В философии для ее обозначения создан специальный термин – эпистемология, или наука о знании.
Я бы хотел начать с первобытных племен далекого прошлого. Стоит отметить, что в каждом из них существовали миф о сотворении мира. По одному древнеяпонскому поверью, некто взболтал грязь, из брызг которой появились острова. Подобные мифы были и у других народов: например, израильтяне верили, что Бог шесть дней творил мир, после чего устал и закончил творение. Все эти мифы схожи – хотя сюжеты их довольно разнообразны, все они пытаются объяснить, почему существует этот мир. Я буду называть такой подход теологическим, поскольку он не предполагает объяснений, кроме как «это произошло по воле богов; они сделали то, что посчитали нужным, и так появился мир».
В районе VI века до н. э. философы античной Греции начали задавать более конкретные вопросы – из чего состоит этот мир, каковы его части, а также попытались подойти к ним скорее рационально, нежели теологически. Как известно, они выделяли стихии: землю, огонь, воду и воздух; у них было еще множество других понятий и убеждений, и медленно, но верно все это преобразовалось в наши современные представления о том, что мы знаем. Тем не менее, тема эта озадачивала людей во все времена, и даже древние греки задавались вопросом, как они знали то, что они знали.
Читать полностью »