Поздравляю всех с (прошедшим) днем числа Пи! (день числа Пи отмечается 14 марта, поскольку эта дата в американском формате записывается в как 3.14 - прим. перев.) Чтобы отметить его как следует, я хочу ненадолго отвлечься от программного обеспечения и поговорить о чем-то особом. Возможно, вы слышали байку о том, как в штате Индиана пытались законодательно приравнять число Пи к чем-то типа 3, или 4, или 3.15. Обычно ее рассказывают в качестве доказательства того, что жители Индианы - бестолковая деревенщина, но это далеко не вся история. Зачем они пытались поменять значение π и на что они рассчитывали?
Рубрика «математика» - 12
Как в Индиане чуть не узаконили π = 3.2
2023-04-15 в 12:50, admin, рубрики: Биографии гиков, доказательство теорем, закон, индиана, математика, мракобесие, Научно-популярное, число пи, эдвард гудвинКак неуловимый «эйнштейн» помог решить давнюю математическую задачу
2023-04-11 в 11:09, admin, рубрики: апериодичность, замощение плоскости, математика, многоугольники, Научно-популярное, плитка, эйнштейн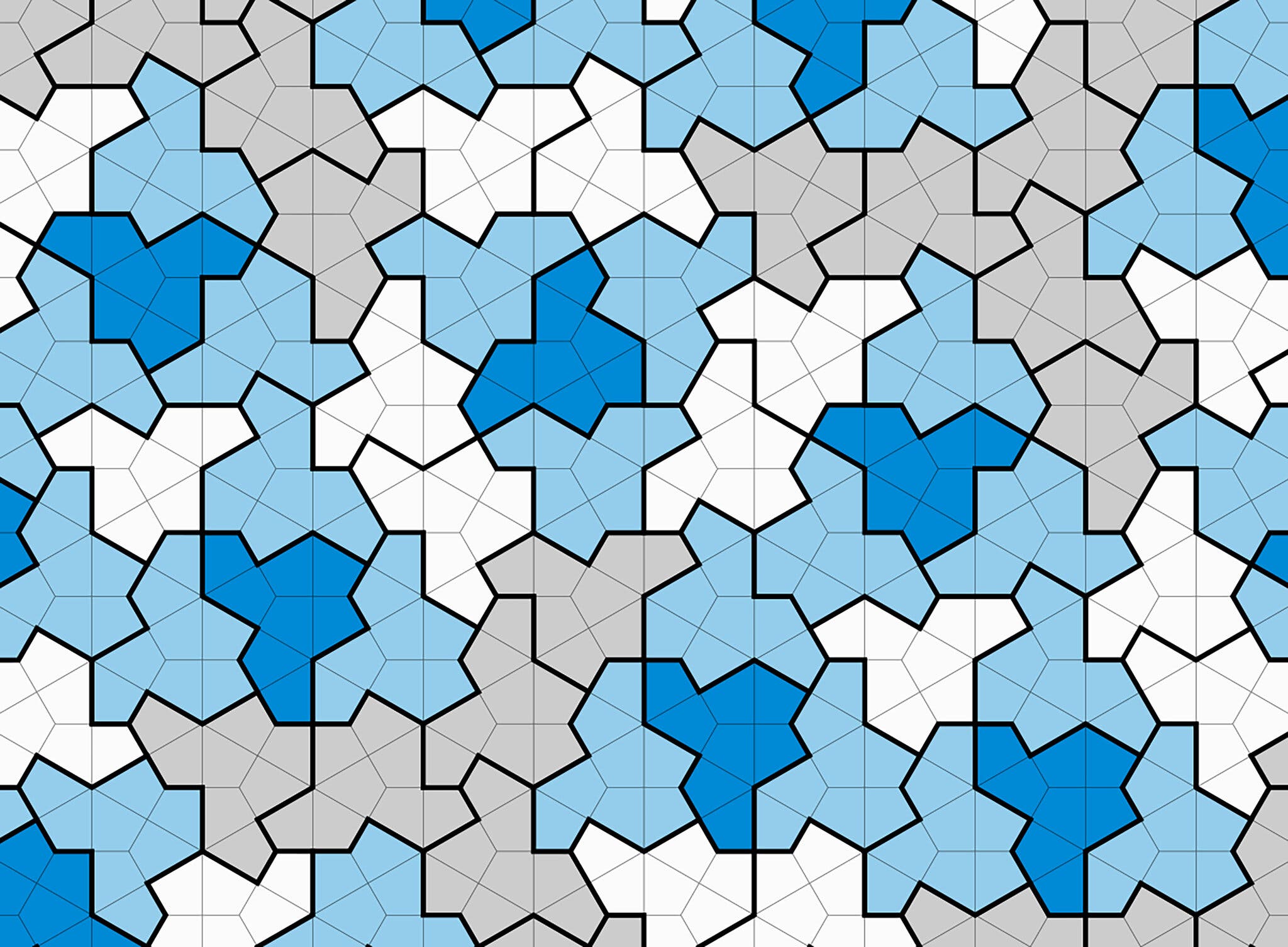
В ноябре прошлого года, после десяти лет неудачных попыток, Дэвид Смит, самопровозглашенный «любитель фигур» из Бридлингтона в Восточном Йоркшире, Англия, заподозрил, что, возможно, он наконец-то решил давнюю задачку в математике замощения плоскости: иначе говоря, он решил, что нашёл «эйнштейна».
В менее поэтичных терминах, «эйнштейн» — это «апериодическая моноплитка», фигура, которая покрывает плоскость или бесконечную двумерную плоскую поверхность неповторяющимся образом. (Термин «эйнштейн» происходит от немецкого «ein stein» или «один камень», в более свободной трактовке — «одна плитка» или «одна фигура»). Ваши обычные обои или кафельный пол представляют собою часть бесконечного узора, который периодически повторяется; при смещении или «переносе» узор может быть точно наложен сам на себя. Апериодическая плитка не обладает такой «трансляционной симметрией», и математики давно ищут единственную фигуру, которая могла бы покрыть плоскость такой плиткой. Эта задача известна под названием «проблемы Эйнштейна».
Читать полностью »
Удивительные кубы Хинтона, которые позволяют каждому увидеть четырехмерный мир
2023-04-09 в 1:35, admin, рубрики: Биографии гиков, геометрия, измерения, математика, наука, фантастикаПриветствую Вас, уважаемые Читатели! Сегодня я хочу рассказать Вам о замечательном популяризаторе математики Чарльзе Говарде Хинтоне - человеке, внесшем просто огромный вклад в дело изучения объектов четырехмерного мира.
Зачем, спрашивается, их изучать? Я, для начала, ограничусь цитатой его тезки Говарда Лавкрафта, произведения которого я не так давно очень полюбил:
Царица наук: математика, беспощадная ты мука
2023-04-08 в 10:22, admin, рубрики: изучаем математику, Лайфхаки для гиков, математика, математика взрослому, мозг, Научно-популярное, Учебный процесс в ITДайджест про то, как и зачем учить математику,
если ты взрослый
Пора забывать GridSearch — встречайте ProgressiveGridSearch. Фракталы в ML, постепенно увеличиваем разрешение
2023-03-31 в 16:18, admin, рубрики: open source, python, искусственный интеллект, математика, машинное обучение, методы оптимизации, нейронные сети, подбор гиперпарметров, сезон machine learningЗдравствуйте, меня зовут Николай Стрекопытов и я придумал как подбирать гиперпараметры бескомпромиссно лучше GridSearch’а. Нужно лишь изменить порядок вычислений. И да, это заявка на обновление индустриального стандарта - скоро вы сможете улучшить свои ML-пайплайны заменой нескольких строчек кода.
Полезные материалы по Data Science и машинному обучению, которые помогут пройти сквозь джунгли из терминов
2023-03-21 в 14:21, admin, рубрики: data engineering, data science, selectel, аналитика данных, Блог компании Selectel, искусственный интеллект, математика, машинное обучение, подборка
Привет! Меня зовут Ефим, я MLOps-инженер в Selectel. В прошлом был автоматизатором, ML-инженером, дата-аналитиком и дата-инженером — и уже несколько лет падаю в пропасть машинного обучения и Data Science. Это буквально необъятная сфера, в которой почти нет ориентиров. Основная проблема в том, что разделов математики довольно много и все они, на первый взгляд, нужны в том же машинном обучении.
В этой статье делюсь полезными материалами, которые помогут найти и заполнить теоретические и практические проблемы и основательно подойти к своему профессиональному развитию. Добро пожаловать под кат!
Читать полностью »
Сообразим на троих. Троичные компьютеры
2023-03-19 в 14:10, admin, рубрики: IT-стандарты, timeweb_статьи_выходного_дня, TriINTERCAL, Блог компании Timeweb Cloud, вычисление, двоичная система счисления, квантовые компьютеры, математика, перфокарта, Программирование, Разработка веб-сайтов, Сетунь, троичная система счисления, эвм
В повседневной жизни мы используем десятичную систему счисления. Почему именно её — это вопрос отдельный. В конце концов, существуют системы с основанием 12 (по фалангам пальцев без большого), 5 (пальцы на одной руке), 20, 60 и так далее. В компьютерах всё несколько проще — там (можно даже сказать, «Традиционно») используется двоичная система, как самая лёгкая для воплощения. Есть ток — нету тока. Есть отверстие в перфокарте — нет отверстия. Ноль или единица. Короче говоря, «да» или «нет» — третьего не дано. А что будет, если дать? Об этом и поговорим.Читать полностью »
Стохастический язык программирования на основе алгоритмов Маркова
2023-03-17 в 5:41, admin, рубрики: марковские цепи, математика, ненормальное программирование, правила замены, Программирование, стохастические алгоритмы
MarkovJunior — это вероятностный язык программирования, в котором программы являются сочетаниями правил перезаписи, а инференс выполняется при помощи распространения ограничений. MarkovJunior назван в честь математика Андрея Андреевича Маркова, придумавшего и исследовавшего то, что сейчас называется алгоритмами Маркова.
Читать полностью »
Генерация 2D мира с помощью клеточного автомата на Python
2023-03-13 в 9:00, admin, рубрики: pygame, python, Алгоритмы, клеточный автомат, математика, пиксель-арт, ПрограммированиеВсем привет! На написание этой статьи меня вдохновил автор YouTube канала PeaAshMeter. В своем видео автор показывает простейший генератор 2D мира, который основан на простейшем правиле клеточного автомата. Что такое клеточный автомат? Какие клеточные автоматы бывают? На эти и многие другие вопросы я попробую ответить.
Проект я решил написать на Python, но поскольку не являюсь экспертом в этой области, то любые замечания, предложения по улучшению кода или проекта — приветствуются!
Пишем игру от первого лица в 2КБ на Rust
2023-03-10 в 7:34, admin, рубрики: raycasting, Rust, webassembly, Wolfenstein 3D, Алгоритмы, математика, разработка игр, рейкастинг
Введение
Поначалу кажется, что создать игру от первого лица без движка или графического API практические невозможно. В этом посте я расскажу, как это сделать при помощи алгоритма под названием ray casting.
Моя цель — показать, что сложную задачу можно разбить на более простые части, и если я всё сделаю правильно, то у вас появится ощущение, что вы сами открыли, как работает игра.
Для начала разберёмся, как работает алгоритм, а затем построчно напишем его. Затем мы пересмотрим код, добавим несколько возможностей и оптимизируем его размер. Я постарался сделать пост максимально доступным и дружелюбным, но вам поможет приличное знание программирования, Rust и основ геометрии.
Читать полностью »
