Осень – самое подходящее время для старшекурсников, чтобы задуматься о планах на следующий учебный год. Вступительные и олимпиады обычно проходят в конце весны/начале лета и есть время для того, чтобы основательно подготовиться. Тем более что экзамены бывают очень непростыми, как, например, в Школу Анализа Данных (ШАД) Яндекса. При поступлении понадобится очень уверенное владение математикой: задачи экзамена носят олимпиадный характер и для успеха мало знаний, нужна еще хорошая насмотренность
Рубрика «матан»
Математика и ШАД
2024-10-06 в 13:16, admin, рубрики: задачи, линал, матан, математика, поступление, теорвер, ШАДСпец-интервью для Хабра: Грант Сандерсон
2021-12-09 в 13:00, admin, рубрики: ruvds_интервью, YouTube, Алгоритмы, Блог компании RUVDS.com, вышка, интервью, линейка, матан, математика, Работа с видео, теорвер, топология
Грант ответил на ваши вопросы. Под катом вы найдёте современный взгляд на обучение математике, тому как правильно применять математику в программировании, и рассказ о том, как превратить простую утилиту для анимации в огромный канал. И конечно же, вас всех ждёт взятие производных на ходу и рассказ о том, как считать первообразные в уме.
Поехали! Читать полностью »
Аналитическое решение уравнений Максвелла: собственные моды оптоволокна (любителям «матана»)
2017-04-12 в 4:25, admin, рубрики: diy или сделай сам, лазеры, матан, оптоволокно, уравнения максвелла, физика, метки: уравнения Максвелла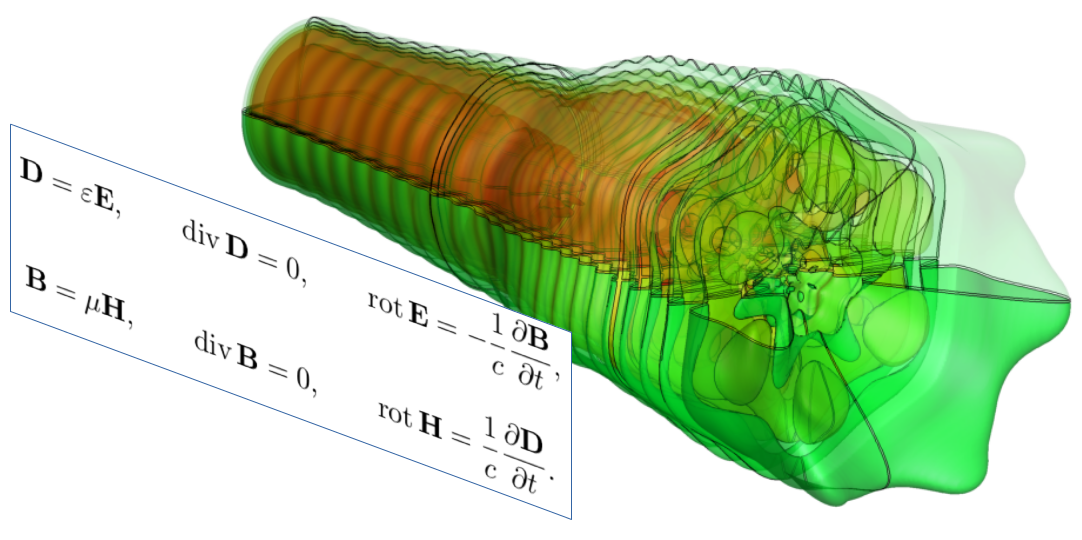
Как-то мне понадобилась "собственная мода оптоволокна". Но я нигде не нашел аналитического выражения электромагнитного поля. Ну и «сделал сам», раз не нашел, и оформил для всех тут, в статье. Так что, скорее всего, нигде больше вы такого не встретите — уникальнейшая вещь! В книжках это не пишут, потому что оно длинное — обычно пишут самое простое, а про общий случай упоминают вскользь. Ну вот он, общий случай, под катом.
Читать полностью »
Хаос внутри судоку
2017-01-08 в 17:13, admin, рубрики: Алгоритмы, выполнимость, диффуры, матан, математика, матлогика, судоку, численные методы
Многие из вас наверняка знакомы с такой головоломкой, как судоку. Возможно, даже реализовывали программу для автоматического решения. На хабре тема судоку обсуждалась уже множество раз, и, как показывает практика, практически любой способ автоматического нахождения ответа в итоге сводится к направленному перебору. И это вполне естественно, ведь даже ручные решения придерживаются тех же принципов. Но что, если поступить иначе?
В данной статье я рассмотрю один очень занятный метод, предложенный в 2012 году, основанный на строго математическом подходе. Программная реализация прилагается.
Трактат об энтропии
2016-08-19 в 5:45, admin, рубрики: матан, термодинамика, физика, химическая термодинамика, химияПриветствую тебя, читатель Гиктаймс!
Многие слышали о такой загадочной штуке, как энтропия. Обычно её называют мерой хаоса, мерой неопределённости и ещё прибавляют, что она непременно растёт. Я с огромной болью переношу употребление имени Энтропии всуе и решил, наконец, написать ликбез по этому вопросу.
Читать полностью »
Использование МатАнализа в компьютерных играх (часть 3)
2016-05-10 в 8:57, admin, рубрики: DPS, wolfram mathematica, Занимательные задачки, заработок в игре, матан, математика, паки в archeage, Программирование, метки: DPSКлючевые слова: DPS (DamagePerSecond); Wolfram Mathematica; дискретность и непрерывность; матанализ; заработок игровой валюты в компьютерных играх; паки ArcheAge.
Введение
Всем знакомы однотипные вопросы в школьных задачах по математике про мотоциклиста выехавшего из пункта А в пункт Б, которые вызывают скуку, отвращение, или просто безразличие. Вопросы, которые вызывают, все что угодно кроме интереса к изучению математики. Очевидно что, гораздо больший интерес и больше эмоций вызывают вопросы типа:
1) «как он смог меня одолеть в игре, если у моего персонажа и здоровья больше и DPS (Damage Per Second) выше?!»
2) «как быстрее всего заработать голду (игровую валюту), чтобы сделать своего персонажа сильнее?!»
На самом деле эти игровые вопросы очень похожи на классические школьные задачи. Разница лишь в том, что есть заинтересованность в получении ответа на игровые вопросы, есть цель, ради которой хочется решить эти задачи. К сожалению, очень многие преподаватели в школах и вузах совершенно не умеют заинтересовать обучаемых в получении конкретной информации, новом методе решений математических задач, доведении их до ответа. Но раз уж игры вызывают этот самый интерес, то грех не воспользоваться заинтересованностью в игре, для пробуждения интереса к математическому анализу.
Вот две задачи, которые являются лишь переформулированными вышеупомянутыми вопросами.
1) Петя и Коля решили помочь дедушке наполнить две одинаковые пустые бочки водой из колодца. Петя таскал воду в 5-и литровом ведре и на один заход к колодцу и обратно к бочке тратил 3 минуты, а Коля в 8-и литровом и на один заход тратил 5 минут. Каждый заполнял свою бочку. Кто из мальчиков быстрее заполнит свою бочку, если а) объём бочки 60 литров? б) если объем бочки 56 литров? (начали мальчики одновременно)
2) Два купца Семён и Добрыня покупают у крестьян по 10 пудов мёда за 5 золотых и везут его на продажу в соседние города. Добрыня везёт в ближайший город и продаёт там за 8 золотых, весь путь до города и обратно у него занимает 2 дня. Семён же, желающий продавать своё мёд как можно дороже, не ленится и везёт его ещё дальше, тратя на весь путь 3 дня, и продавая мёд в другом городе за 10 золотых. Кто же из купцов заработает больше за 360 дней непрерывной работы? Как изменится ситуация, если оба купца вынудят крестьян снизить цену на мёд до 3 золотых?
Разбор этих задач, описанный ниже, поможет ответить на животрепещущие вопросы игры ArcheAge (и других) про «паки» и DPS. А также позволит задуматься над такими понятиями как «дискретность» и «непрерывность», а так же над таким, казалось бы, очевидным вопросом как «прибыль».
Читать полностью »
Использование МатАнализа в компьютерных играх (часть 2)
2016-01-11 в 6:35, admin, рубрики: ArcheAge, Wolfram Alpha, wolfram mathematica, Задача о коллекции, матан, математика, Программирование, числа Стирлинга второго рода, метки: Задача о коллекцииКлючевые слова: Задача о коллекции; Wolfram Alpha; Wolfram Mathematica; числа Стирлинга второго рода; матанализ; теория вероятностей; мат ожидание; медиана; квантиль; компьютерные игры; коллекция вкладышей; функция распределения случайной величины; плотность вероятности, ArcheAge.
Введение
Когда остается заполучить только три из ста предметов для того чтобы собрать всю коллекцию (вкладышей жвачек БомБимБома или Турбо, или набора тяжелых доспехов для персонажа компьютерной игры), то огонь в глазах и ожидание чуда вытесняют и логику и разум и попытки математического анализа из головы напрочь. Есть только одна мысль «Ещё чуть-чуть и я заполучу оставшееся! Я соберу всю!». В это время, родные и друзья, этого одержимого коллекционера озадачены лишь только одним вопросом – «А, чуть-чуть, это сколько?!». Сколько маме нужно купить ещё ненавистных жвачек, или сколько нужно ещё девушке сидеть одной, пока её парень не выбьет с монстров в игре «редчайшие трусы Баала»?!
Ответить на вопрос «сколько нужно купить жевательных резинок, чтобы собрать полную коллекцию из N-штук вкладышей» сходу довольно сложно, даже если пользоваться Яндексом, потому, что сложно сформулировать сам запрос для «обычного» поисковика. Попытка решения задачи самостоятельно обычно ставит людей в тупик – не понятно, с какой стороны к ней подступиться.
В данной статье будут рассмотрены три вопроса: Как подходить к задачам, которые не понятно на первый взгляд как решать? Каким поисковиком пользоваться для того чтобы получать научные ответы на научные вопросы (а не получать предложения купить формулу квадратного уравнения на eBay)? И конечно, сколько же нужно купить жвачек, чтобы собрать коллекцию вкладышей?
Читать полностью »
Unreal Engine применили для моделирования роста нанолеса
2013-12-27 в 7:04, admin, рубрики: game development, Unreal Engine, матан, нанотехнологии, Научно-популярное, метки: Unreal Engine, матан Группа учёных из Канады провела моделирование роста разветвлённых нанопроволок (нанодеревьев) весьма оригинальным способом — вместо специализированных научных кодов они взяли коммерческий игровой движок.
Читать полностью »
Нескучные интегралы
2013-11-02 в 14:37, admin, рубрики: интегралы, матан, математика, преобразование фурье, метки: интегралы, матан, математика, преобразование фурье Некоторые из вас, вероятно, видали на просторах сети эту задачку: какое число продолжает следующий ряд?
Предлагался такой очевидный правильный ответ:
Для тех, кому неочевидно, как он получен, предлагалось объяснение. Пусть 
(ну и 1 при x = 0, хотя неважно). Тогда каждый член ряда — это значение следующего интеграла в цепочке:
Пока всё идёт хорошо, но тут внезапно:
В принципе, этого достаточно, чтобы повеселить друзей-математиков, но мне захотелось узнать, как вообще считаются такие интегралы и почему получается такой смешной результат. Если кому-то ещё охота тряхнуть стариной и вспомнить матан с функаном, прошу читать дальше.Читать полностью »
О критерии Лебега, или В чем была ошибка Кэрролла
2013-01-28 в 4:27, admin, рубрики: кэрролл, матан, математика, метки: кэрролл, матан 
Прочитав пост «Ломаем спички», я равнодушно пожал плечами. Это ж тривиальная задачка о непрерывности функций, мелкое развлекалово для третьего курса матфака. Есть и более весёлые её варианты, к примеру, тот, что на картинке слева.
К моему удивлению, обсуждение перевалило за 200 комментов, а слова «критерий Лебега» так и не прозвучали. Ну что же, придётся исправлять это недоразумение.
Disclaimer: т.к. набирать с клавиатуры математические формулы чудовищно неудобно, я буду писать пределы вот так: limn → ∞ f(x), а интегралы вот так a∫bf(x)dx. Уж извините.