Плитки (домино) Вана были изобретены Хао Ваном в 1961 году для математических задач, но нашли широкое применение в играх при создании тайловой графики. Благодаря им результаты не выглядят повторяющимися, как в 2D-текстурах, так и в 3D-моделях с тайлингом.
Похоже, что плитки Вана также способны исполнять машины Тьюринга, и следовательно, они Тьюринг-полны, а значит, могут выполнять любую программу.
Это удивительное и непонятное заявление, поэтому в данном посте я немного исследую этот вопрос.
Вкратце о плитках Вана
Плитки Вана — это прямоугольные тайлы, у которых каждая из граней может соответствовать только другим конкретным граням, но для любой конкретной грани есть несколько возможных тайлов, которые могут соответствовать этой грани. Под соответствием граней я подразумеваю, что они соединяются бесшовно, не создавая никаких визуальных артефактов и признаков наличия шва между тайлами.
Это полезное для графики свойство, потому что оно позволяет создавать бесшовную тайловую графику, но конфигурация расположения тайлов при этом может быть полностью рандомизирована при условии, что все грани совместимы друг с другом. В результате получается тайловая графика, которая совсем не похожа на повторяющуюся, потому что визуальные паттерны становятся гораздо менее заметными, чем у традиционной тайловой графики.
Графические примеры, более подробную информацию и ссылки на Shadertoy можно найти здесь: Wang Tiling.
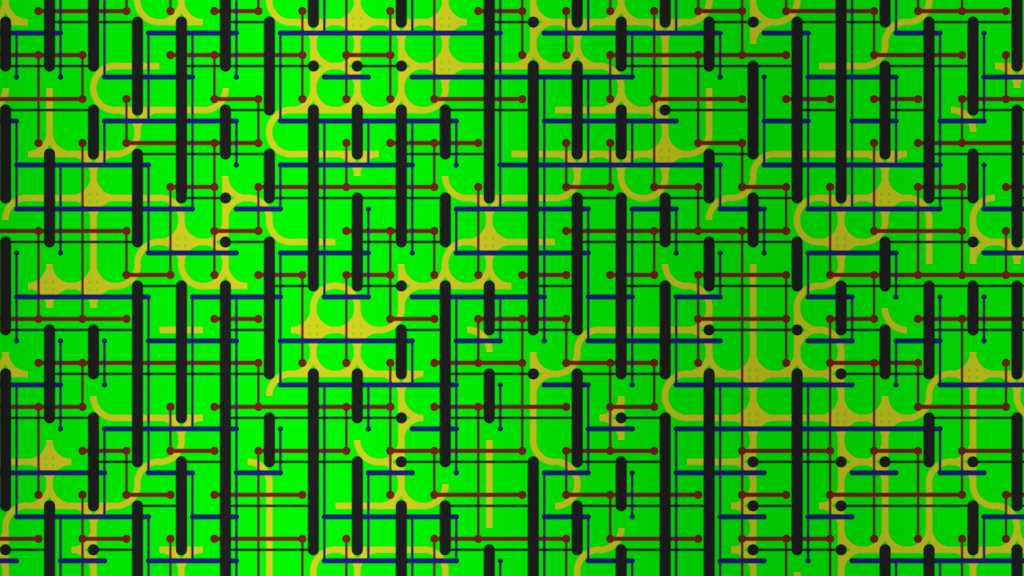
Вот созданный мной пример. Моя графика — это «арт программиста», но надеюсь, идея понятна. Рисунок составлен из 16 тайлов, и для каждой грани есть два различных типа граней.