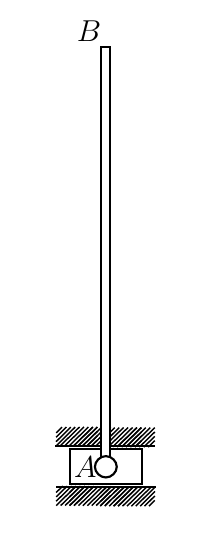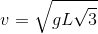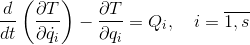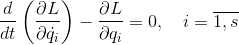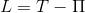Предисловие
По роду профессиональной и научной деятельности я механик. Преподаю теоретическую механику в университете, пишу докторскую диссертацию в области динамики подвижного состава железных дорог. В общем, эта наука поглощает большую часть моего рабочего и даже свободного времени.
С Maple (на кафедре была 6-я версия, а у лоточников домой была куплена 8-я) познакомился ещё студентом, когда начинал работать над будущей кандидатской под крылом моего первого (ныше покойного) научного руководителя. Были и добрые люди, что помогли на самом первом этапе разобраться с пакетом и начать работать.
И вот так постепенно на его плечи была переложена большая часть вычислительной работы по подготовке диссертации. Диссертация была защищена, а Maple навсегда остался надёжным помошником в научном труде. Часто бывает необходимо быстро оценить какую-нибудь задачу, составить уравнения, исследовать их аналитически, быстро получить численное решение, построить графики. В этом отношении Maple просто незаменим для меня (ни в коем разе не хочу обидеть приверженцев других пакетов).
Сделать всё то, что будет предложено читателю под катом, меня задача принесенная ученицей (приходится ещё заниматься и репетиторством) со школьной олимпиады. Условие задачи таково:
Груз, висящий на нити длины L = 1,1 м, привязанной к гвоздю, толкнули так, что он поднялся, а затем ударился в гвоздь. Какова его скорость в момент удара о гвоздь? Ускорение свободного падения g = 10 м/с2.
Если не придираться к некоторонной туманности условия, то задача достаточно проста, а её решение, полученное путем довольно громоздких для школьника выкладок, в общем виде дает результат
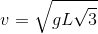
И вот тут захотелось проверить решение, полученное с оглядкой на школьную программу по физике независимым способом, например составив дифференциальные уравнения движения этого маятника, да не просто, а с учетом освобождения от связи (в процессе движения нить, считаемая невесомой, провисает и маятник движется как свободная точка).
Это послужило катализатором для того, чтобы взять да и откопать свои старые задумки, накопленные ещё со времен работы в оргкомитете Всероссийской Олимпиады студентов по теоретической механике — три года подряд занимался там подготовкой задач компьютерного конкурса. Задумки касались автоматизации построения уравнений движений для механических систем с неудерживающими связями и трением, используя известные всем уравнения Лагранжа 2 рода
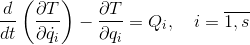
поборов стереотип многих преподавателей о том, что уравнения эти неприменимы к системам с неудерживающими связями и трением.
Что касается Maple, то его библиотека для решения задач вариационного исчисления дает возможность быстро получить уравнения Эйлера-Лагранжа, решение которых минимизирует действие по Гамильтону, что применимо для консервативных систем
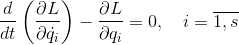
где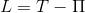 
— функция Лагранжа, равная разности кинетической и потенциальной энергий системы.
Так как расматриваемые задачи не относятся к классу консервативных, то автором была предпринята попытка самостоятельно реализовать автоматизацию построения и анализа уравнений движений. Что из этого вышло, изложено под катом
Читать полностью »
