Введение
Возможно, кто-то задаст вопрос, а причем тут математика? Отвечу сразу: все, что здесь изложено, относится непосредственно к математике.
Изучая литературу по теории построения моделей предметной области, я обнаружил серьезный пробел. Авторы статей и книг сразу берут одну из нотаций моделирования: ER-диаграммы, или диаграммы классов, и в быстром темпе начинают их использовать для описания предметной области. При этом описание парадигмы, в которой производится это моделирование остается вообще не раскрытым. А следовательно, не раскрытыми остаются ограничения той или иной нотации. Увы, мы все умеем строить модели, но мало кто умеет объяснить то, что он построил в одной из существующих парадигм. Поэтому я часто слышу дикие с точки зрения любой парадигмы термины: класс типов, типы классов, виды типов и так далее, но ни разу не слышал корректный термин «класс классов». Этот пробел в нашем образовании очень серьезен. И я объясню почему.
Давайте зададим аналитикам простой вопрос.
Те, кто моделировал процессы, наверно, знакомы с нотацией BPMN. Очень часто при моделировании операции по заключению договора я встречаю такой фрагмент диаграммы:
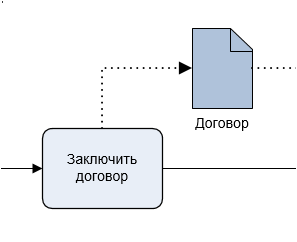
Видно, что в результате заключения договора рождается нечто, что передается в другую операцию. Но что обозначает элемент диаграммы в виде листа с загнутым уголком? Нам надо точно знать, что именно передается из одной операции в другую, иначе трудно будет объяснить другим, что от них требуется. Итак, что создается на выходе из операции «Заключить договор»?
Варианты ответов, которые я слышал, следующие:
- Бумажка с печатью
- Бумажки с печатью
- Класс бумажек с печатью
- Договор
- Договоренность
- Информация о договоренности
- Файл MS Word с названием договор
- Запись в базе данных
- Поток каких-то объектов
Пока я наблюдаю отсутствие согласия между аналитиками на предмет того, что же все-таки передается, и что значат термины «договор», «поток», «договоренность», «информация», «данные». Чтобы ответить на этот вопрос, мне пришлось копать глубоко и в сторону парадигм. Причем, ответ потребовал разбиения вопроса на два. Первый вопрос был: «Как корректно сформулировать вопрос?» А второй был: «Как на него ответить?». Для правильной формулировки нужно было выбрать подходящую парадигму. Эта статья посвящена рассказу о двух парадигмах: Аристотелевской и логической, и почему я выбрал логическую в качестве рабочей. Ответа на поставленный вопрос в этой статье я не дам. Ответ я дам в другой статье.
Читать полностью »