Применение машинного обучения может включать работу с данными, тонкую настройку уже обученного алгоритма и т. д. Но масштабная математическая подготовка нужна и на более раннем этапе: когда вы только выбираете модель для дальнейшего использования. Можно выбирать «вручную», применяя разные модели, а можно и этот процесс попробовать автоматизировать.
Под катом — лекция ведущего научного сотрудника РАН, доктора наук и главного редактора журнала «Машинное обучение и анализ данных» Вадима Стрижова, а также большинство слайдов.

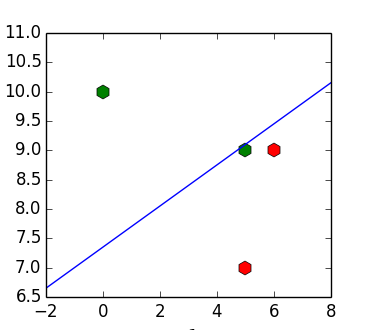
![Зачем нужен алгоритм Хо-Кашьяпа? - 1 X=[(6, 9), (5, 7), (5, 9), (10, 1)]](https://www.pvsm.ru/images/2016/10/16/zachem-nujen-algoritm-ho-kashyapa.)
![Зачем нужен алгоритм Хо-Кашьяпа? - 2 y=[1, 1, -1, -1]](https://www.pvsm.ru/images/2016/10/16/zachem-nujen-algoritm-ho-kashyapa-2.)