Работа с числовыми матрицами в целом и решение систем линейных алгебраических уравнений в частности — классическая математическая и алгоритмическая задача, широко используемая при моделировании и расчёте огромного класса бизнес-процессов (например, при расчёте себестоимости). При создании и эксплуатации конфигураций «1С:Предприятия» многие разработчики сталкивались с необходимостью вручную реализовывать алгоритмы расчёта СЛАУ, а после — с проблемой длительного ожидания решения.
«1С:Предприятие» 8.3.14 будет содержать функционал, позволяющий значительно сократить время решения систем линейных уравнений за счёт использования алгоритма, основанного на теории графов.
Он оптимизирован для использования на данных, имеющих разреженную структуру (то есть содержащие не более 10% ненулевых коэффициентов в уравнениях) и в среднем и в лучшем случаях демонстрирует асимптотику Θ(n⋅log(n)⋅log(n)), где n — количество переменных, а в худшем (при заполненности системы ~100%) его асимптотика сопоставима с классическими алгоритмами ( Θ(n3)). При этом на системах, имеющих ~105 неизвестных, алгоритм показывает ускорение в сотни раз по сравнению с реализованными в специализированных библиотеках линейной алгебры (например, superlu или lapack).
Важно: статья и описанный алгоритм требуют понимания линейной алгебры и теории графов на уровне первого курса университета.
Читать полностью »
Рубрика «линейная алгебра» - 2
Как мы в «1С: Предприятии» решаем системы алгебраических уравнений
2018-08-14 в 8:12, admin, рубрики: 1С, Алгоритмы, Блог компании 1С, линейная алгебра, линейные уравнения, математика, СЛАУGFDM и тензоры. Продолжение
2016-11-28 в 6:48, admin, рубрики: gfdm, будущее здесь, линейная алгебра, математика, Научно-популярное, обработка данных, сотовая связь, тензоры, метки: GFDM и тензоры. Продолжение / Geektimes @font-face{font-family:'Fira Sans';font-style:normal;font-weight:400;src:url(/fonts/0/FiraSans/hg-FiraSans-Regular.eot);src:local("Fira Sans"), local("FiraSans-Regular"), url(/fonts/0/FiraSans/hg-FiraSans-Regular.eot?#iefix) format("embedded-opentype"), url(/fonts/0/FiraSans/hg-FiraSans-Regular.woff) format("woff"), url(/fonts/0/FiraSans/hg-FiraSans-Regular.woff2) format("woff2")Сначала я хотел не углубляться в тензоры и описать их мимоходом, касаясь только используемого мной функционала. Однако я изменил свое мнение и решил рассказать больше. Добро пожаловать в многомерный мир.
Читать полностью »
Тензорные разложения и их применения. Лекция в Яндексе
2016-10-30 в 14:39, admin, рубрики: Matlab, python, TensorFlow, Алгоритмы, Блог компании Яндекс, линейная алгебра, математика, матрицы, многомерный массив, ненормальное программирование, разложение, тензорыПредыдущая лекция с Data Fest была посвящена алгоритмам, необходимым для построения нового вида поиска. Сегодняшний доклад тоже в некотором смысле про разные алгоритмы, а точнее про математику, лежащую в основе множества из них. О матричных разложениях зрителям рассказал доктор наук и руководитель группы вычислительных методов «Сколтеха» Иван Оселедец.
Под катом — расшифровка и большинство слайдов.
Так ли быстр ваш любимый С или нативная реализация линейной алгебры на D
2016-10-03 в 6:46, admin, рубрики: C, D, Eigen, Intel MKL, LDC, machine learning, Mir GLAS, OpenBLAS, opencv, Алгербра, линейная алгебра, машинное обучениеТем, кто занимается системами машинного обучения и компьютерным зрением, хорошо знакома такая библиотека как OpenBLAS (Basic Linear Algebra Subprograms). OpenBLAS написан на C и используется повсеместно там где нужна работа с матрицами. Так же у него есть несколько альтернативных реализаций таких как Eigen и двух закрытых имплементацией от Intel и Apple. Все они написаны на СС++.
В настоящий момент OpenBLAS используется в матричных манипуляциях в таких языках как Julia и Python (NumPy). OpenBLAS крайне хорошо оптимизирована и значительная её часть вообще написана на ассемблере.
Однако так ли хорош для вычислений чистый C, как это принято считать?
Встречайте Mir GLAS! Нативная реализация библиотеки линейной алгебры на чисто D без единой вставки на ассемблере!
Читать полностью »
От действий над матрицами к пониманию их сути…
2016-02-17 в 14:04, admin, рубрики: линейная алгебра, математика, математика на пальцах, матрица, определительОчень уважаю людей, которые имеют смелость заявить, что они что-то не понимают. Сам такой. То, что не понимаю, — обязательно должен изучить, осмыслить, понять. Статья "Математика на пальцах", и особенно матричная запись формул, заставили меня поделиться своим небольшим, но, кажется, немаловажным опытом работы с матрицами.
Лет эдак 20 назад довелось мне изучать высшую математику в вузе, и начинали мы с матриц (пожалуй, как и все студенты того времени). Почему-то считается, что матрицы — самая лёгкая тема в курсе высшей математики. Возможно — потому, что все действия с матрицами сводятся к знанию способов расчёта определителя и нескольких формул, построенных — опять же, на определителе. Казалось бы, всё просто. Но… Попробуйте ответить на элементарный вопрос — что такое определитель, что означает число, которое вы получаете при его расчёте? (подсказка: вариант типа «определитель — это число, которое находится по определённым правилам» не является правильным ответом, поскольку говорит о методе получения, а не о самой сути определителя). Сдаётесь? — тогда читаем дальше...Читать полностью »
Mathcad Express — бесплатный математический редактор, про который мало кто знает
2015-02-05 в 13:05, admin, рубрики: Mathcad Express, Mathcad Prime, MOOC, Блог компании Нерепетитор.ру, вычисление интеграла, график, данные, косинус, линейная алгебра, математика, математический анализ, матрица, МООС, расчет, синус, метки: Mathcad Express, вычисление интегралаПрежде всего, приветствую первых посетителей моего блога. Это моя первая статья на Хабре и я надеюсь, что смогу рассказать вам здесь много полезного.
РТС Mathcad – это характерный пример математического ПО, предназначенного для осуществления, как численных, так и аналитических расчетов по формулам и визуализации их результатов в виде графиков.Читать полностью »
Краткий курс компьютерной графики: пишем упрощённый OpenGL своими руками, статья 3.14 из 6
2015-01-30 в 19:55, admin, рубрики: c++, линейная алгебра, Программирование, Работа с анимацией и 3D-графикойСодержание основного курса
- Статья 1: алгоритм Брезенхэма
- Статья 2: растеризация треугольника + отсечение задних граней
- Статья 3: Удаление невидимых поверхностей: z-буфер
- Статья 4: Необходимая геометрия: фестиваль матриц
- Статья 5: Пишем шейдеры под нашу библиотеку
- Статья 6: Чуть больше, чем просто шейдер: просчёт теней
Улучшение кода
- Статья 3.1: Настала пора рефакторинга
- Статья 3.14: Красивый класс матриц
- как работает новый растеризатор
4 Приветствие и вступление
Нумерация в прошлой статье закончилась на 3, в этой будем продолжать нумеровать насквозь.
UPD: ВНИМАНИЕ! Раздел, начиная с номера 3.1, 3.14 и 3.141 и далее, будет о тонкостях реализации основы основ компьютерной графики — линейной алгебры и вычислительной геометрии. О принципах графики пишет haqreu, я же буду писать о том, как это можно внятно запрограммировать!
Эта статья является продолжением серии статей о практической реализации элементов вычислительной геометрии, и, в частности, программного отрисовщика, с использованием C++98. Мы с haqreu сознательно идем на использование прошлой версии стандарта и написание собственной геометрической библиотеки для того, чтобы, во-первых, выпустить код примеров, которые без особых трудностей будут компилироваться большинством имеющихся компиляторов, а во-вторых, чтобы в нашем коде не было ничего, что скрыто в недрах библиотеки. В статье излагаются вопросы реализации шаблона прямоугольной матрицы template<size_t DimRows,size_t DimCols,typename number_t> class mat;
4.1 Благодарности
Я выражаю огромную признательность haqreu, как основоположнику данного курса. Так держать!
Я очень признателен lemelisk за предварительное рецензирование и ревью моих исходников. Спасибо за плодотворные дискуссии!
Читать полностью »
Краткий курс компьютерной графики: пишем упрощённый OpenGL своими руками, статья 3.1 из 6
2015-01-26 в 21:41, admin, рубрики: c++, game development, линейная алгебра, Программирование, Работа с анимацией и 3D-графикойСодержание курса
- Статья 1: алгоритм Брезенхэма
- Статья 2: растеризация треугольника + отсечение задних граней
- Статья 3: Удаление невидимых поверхностей: z-буфер
- Статья 3.1: Настала пора рефакторинга
- Статья 4: Необходимая геометрия: фестиваль матриц
- Статья 5: Пишем шейдеры под нашу библиотеку
- Статья 6: Чуть больше, чем просто шейдер: просчёт теней
Данная статья написана в тесном сотрудничестве (спасибо создателям XMPP) с haqreu, автором данного курса.Мы начали масштабный рефакторинг кода, направленный на достижение максимальной компактности и читаемости. Мы сознательно пошли на отказ от ряда возможных и даже очевидных оптимизаций для получения максимально доступного для понимания кода учебных примеров.
P. S haqreu буквально на днях выложит статью о шейдерах!
Читать полностью »
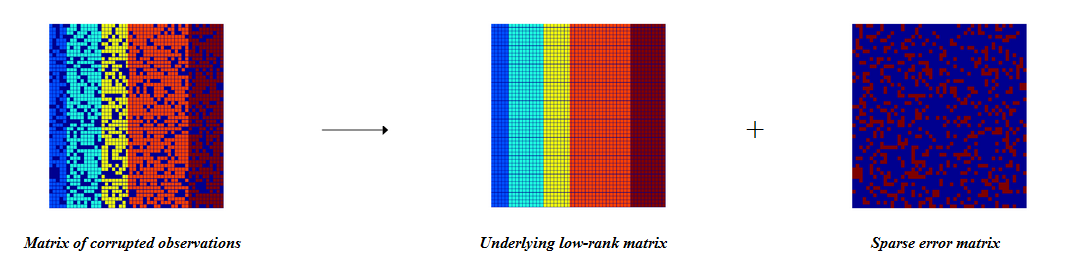
Алгоритм TILT или нестандартное использование ранга матрицы
2014-12-10 в 10:18, admin, рубрики: computer vision, линейная алгебра, методы оптимизации, обработка изображений Сегодня мы рассмотрим алгоритм TILT (Transform Invariant Low-rank Texture) и множество его методов применения в области Computer Vision. Статья будет нести несколько обзорный характер, без плотного углубления в математические дебри.
Читать полностью »
Решение СЛАУ с матрицей общего вида
2013-06-13 в 14:07, admin, рубрики: алгебра, Алгоритмы, линейная алгебра, математика, Программирование, Система линейных уравнений, метки: алгебра, линейная алгебра, математика, Программирование, Система линейных уравненийРассмотрим систему линейных алгебраических уравнений (СЛАУ) из m уравнений с n неизвестными:
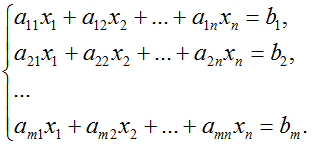
Матрица системы может быть не только квадратной невырожденной, но и квадратной вырожденной или прямоугольной.
Требуется найти все решения данной системы либо определить, что она несовместна (не имеет решений).
Рассмотрим метод Гаусса решения СЛАУ.
Читать полностью »