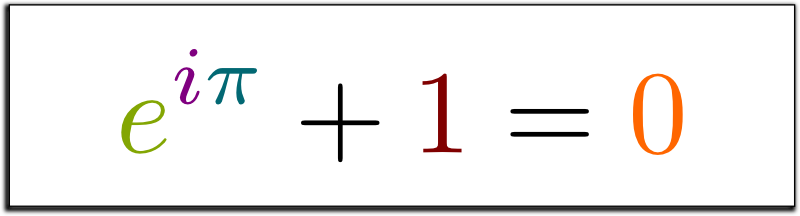Стоит открыть исходники любого современного игрового движка – неважно, это C++-рендер, сделанный на коленке, или какая-нибудь гигантская экосистема вроде Unity или Unreal Engine – вы первым делом натыкаетесь на одни и те же знакомые сущности. Все вокруг живет в Vector3: координаты, направления движения, точки столкновений. Каждая частица указывает, куда она смотрит, с помощью Quaternion. А если требуется что-то покруче – переносить и одновременно крутить объект, то Matrix4x4Читать полностью »
Рубрика «кватернионы»
Почему мы до сих пор неправильно пишем физические движки и 3D-графику
2026-06-17 в 14:05, admin, рубрики: Gamedev, python, timeweb_статьи, внешнее произведение, геометрическая алгебра, игровые движки, кватернионы, конформная геометрия, мультивекторПрактическая сторона кватернионов для описания вращений
2026-06-05 в 7:35, admin, рубрики: unity, кватернионы, математика, математические модели, математические моделированиеНаверняка те из вас, кто работал с Unity, Unreal Engine, ThreeJS или просто интересовался компьютерной графикой, слышали слова «матрица поворота», «кватернион», «углы Эйлера» и тому подобное.
Давайте объединим линейную и геометрическую алгебры. На простом примере. Часть 1
2026-02-23 в 6:00, admin, рубрики: алгебра клиффорда, векторы, геометрия, кватернионы, матрицы, матрицы паулиПривет!
Если вы когда-нибудь решали школьные задачи с параллелограммом, то знаете: найти все стороны, углы, диагонали, да ещё и опустить на них высоты — возни много. А потом ещё проверить, не перепутал ли ты, где синус, а где косинус.
Оказывается, всю эту геометрию можно упаковать в одну маленькую матрицу 2×2. Буквально: берем два вектора-столбца, составляем матрицу — и в ней уже зашиты все возможные характеристики фигуры. Осталось только научиться их оттуда доставать.
В конце статьи описан базис Клиффорда для матриц 2х2
Единая теория всего… в 3D графике? Разбираем алгебру Клиффорда как универсальный язык геометрии
2025-11-04 в 5:01, admin, рубрики: алгебра клиффорда, векторы, вращения, геометрическая алгебра, геометрия, кватернионы, комплексные числа, матрицы паули, отражения, физикаПривет!
Мы, программисты, инженеры и физики, привыкли к своему зоопарку математических инструментов. Векторы — для направлений и позиций. Матрицы — для трансформаций. Кватернионы — для вращений без головной боли с блокировкой осей. Комплексные числа — для 2D-поворотов и обработки сигналов. Каждый инструмент хорош для своей задачи, но мы постоянно переключаемся между ними, преобразуя данные и жонглируя концепциями.
А что, если я скажу вам, что существует единый математический объект, который может быть всем этим одновременноЧитать полностью »
«Разработка алгоритма программного управления пространственной ориентацией КА»
2025-11-01 в 10:15, admin, рубрики: кватернионы, МКА, ориентацияКраткая история комплексных чисел
2025-09-26 в 11:00, admin, рубрики: быстрое преобразование фурье, кватернионы, комплексные числа, шрёдингер
Почему векторное произведение существует только в R^0, R^1, R^3, R^7?
2025-08-26 в 15:20, admin, рубрики: векторное произведение, кватернионы, октонионы, скалярное произведениеЧаще всего с векторным произведением мы знакомимся в курсе аналитической геометрии, где мы редко выходим в задачах за размерность три, поэтому может складываться впечатление, что векторное произведение обобщается на любую размерность, по аналогии со скалярным.
Вспомним, что такое векторное произведение векторов. Векторным произведением векторов Читать полностью »
Метафизика мнимой единицы
2025-07-05 в 12:36, admin, рубрики: кватернионы, комплексные числа, наука складности, фазовый законПрочитав [1], хотя это и не академический материал, очень впечатлился идеей того, что мнимая единица 
кодирует направление. Дело в том, что если мы имеем в формуле два скаляра, которые запрещено складывать и это - в математике, которая запросто суммирует апельсины с помидорами, происходящее должно нести какой-то смыслЧитать полностью »
Геометрический смысл комплексного гармонического осциллятора и винты
2025-06-09 в 6:00, admin, рубрики: алгебры клиффорда, геометрия, кватернионы, комплексные числа, ТФКПАннотация: Исследуется связь комплексных решений уравнения гармонического осциллятора с винтовыми движениями. Показано, что суперпозиция решений с противоположной хиральностью описывает синхронизированные линейные и вращательные колебания в системе "груз-пружина".
И что отдельно интересно, это то, что в очередной раз оказалось невероятно удобно работать с нейросетью DeepSeek:
-
Получилось сначала обсудить с ней идею, за пол дня, написав ей подобие промптов, а она в конце написала мне промпт, как для другой нейросети, над чем мне подумать.
Простыми словами о углах Эйлера, Кватернионах и матрицах поворота в Unity
2025-04-28 в 14:15, admin, рубрики: unity, unity уроки, unity3d, unity3d уроки, вектор, кватернионы, матрицы, углы ЭйлераВ этой статье мы поговорим о математических основах вращения объектов, Эйлеровых углах и проблематике их использования, а также о Кватернионах и причинах выбрать Кватернионы перед Эйлеровыми углами.
Математические основы вращения объектов
На базовом математическом уровне существует следующая формула: